
备份的历史
亚历⼭⼤图书馆
印刷机的诞⽣
磁带备份系统 Tap backup systems
另⼀种形式的备份:纠删码
需要了解的知识点:
错误检测 Error Detection
如果没有错误检测
错误检测技术的原理
奇偶校验 Parity Checking
举例说明(数据发送⽅)
举例说明(数据接收⽅)
奇偶校验的缺点:校验位翻转
奇偶校验的缺点:多⽐特错误
错误检测的游戏
校验和算法 Checksum
Logic Puzzles
汉明码 Hamming-Code
汉明码的⼯作原理
拆解汉明码验证过程
汉明码⽆法检测的情况
汉明码总结
RAID 5 与汉明码
⾥德·所罗门编码 The Reed-Solomon Code
多项式插值(Polynomial interpolation)
伽罗⽡域(Galois Field)
举例: GF(2^3)=0,1,2,3,4,5,6,7
⾥德所罗门编码的应⽤
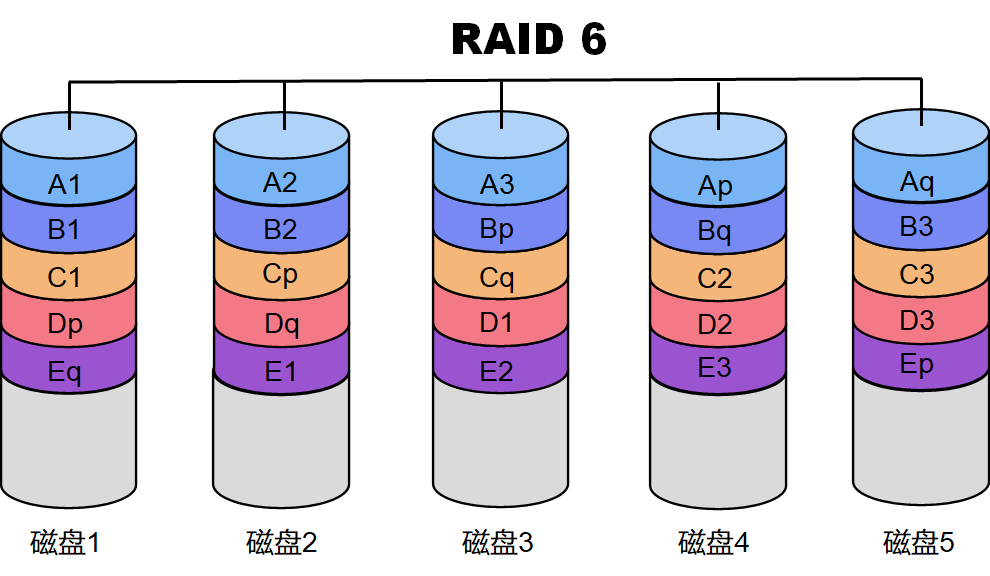
RAID 6 与⾥德所罗门编码
常⻅的 RAID6 术语
RAID6 中的7种硬盘损坏情况
使⽤ Python 验证 RAID5/6
1.设定3块盘的初始数据
2.⽣成PD盘的奇偶校验数据
假设此时数据盘D3损坏(RAID5 恢复原理)
3.⽣成伽罗⽡域
4.定义伽罗⽡域的操作
5.⽣成 RS 盘的纠删码
6.五块盘的初始数据⽣成完毕
演⽰磁盘损坏后还原数据
同时损坏1块数据盘和1块PD盘
同时损坏两块数据盘
文章篇幅较长,请耐心看完!!
备份的历史
任何从事IT⾏业的相关⼈员都会熟练的使⽤“复制+粘贴”的⽅式来备份数据。
但在⾮数字世界中,历史上最早的备份技术是:印刷机(printing press)
亚历⼭⼤图书馆
亚历⼭⼤图书馆(Library of Alexandria)是世界上最古⽼的图书馆之⼀,馆内收藏了贯穿公元前400-前300年时期的⼿稿,拥有最丰富的古籍收藏,因此
亚历⼭⼤图书馆也被称为“地中海⽂明的太阳”

但随着⼀场战⽕将图书馆摧毁,⼤量有价值的⽂献从这个世界上永远消失了。

要如何再次避免这种情况发⽣?
印刷机的诞⽣
印刷术的诞⽣改变了这种情况。
印刷术允许制作完整的、相同的(或接近相同)书籍副本,并在其他物理位置上进⾏保存,这使得⼀部珍贵书籍丢失的可能性⼤⼤降低。

但是,世界上⼏乎没有⼀个图书馆有⾜够⼤的空间⽤于保存其他图书馆书籍的“完整备份”。
也许…如果你要抬杠的话,可能还真有⼀个…
世界上最⼤的图书馆:美国国会图书馆(Library of Congress)

国会图书馆收藏约 1.7 亿份藏品
⽽根据 bing 搜索,全世界⼤约只有 1.3亿本书
⾸先不考虑国会图书馆本⾝的书籍如何备份;国会图书馆的建造费⽤⾼达650万美元,并且还需聘请⼏千个⼯作⼈员以及维护书籍的开销,如果还想随着
时间的变化,不断保存书籍的最新副本,那么国会图书馆的空间迟早也会消耗殆尽。
磁带备份系统 Tap backup systems
部分企业为了防⽌存储空间不⾜,会使⽤磁带备份系统来备份⼤量的”inactive”和”cold data”数据,这些数据可能在之后的⼏年内都不会再被访问。
*注:使⽤磁带备份也有⼀些问题,如访问速度慢、安装成本⾼、温度湿度导致的介质损坏等…

另⼀种形式的备份:纠删码
纠删码 erasure coding,是数据存储中的核⼼概念。
核⼼原理: 于其维护⼀个数据的完整副本,不如将数据分解成⼀组⽚段,在原始数据丢失的情况下,可以通过剩余的⽚段重新构建原始数据。
听起来与磁盘的 RAID 条带化技术相似,但纠删码避开了 RAID 技术所⾯临的许多问题
需要了解的知识点:
错误检测 Error Detection
早在现代计算机发明之前,数学家们就在研究:“如何确保传输的数据在收到之后能被验证的技术” 换句话说,我们能不能知道接收到的信息是否是完整⽆
缺的到达我们⼿中?
下图是⼀个经典的使⽤错误检测的游戏:

如果没有错误检测

存储或传输信息的设备经常发⽣故障,如:链路上的⼲扰,⼈为的误操作、数据总线的噪⾳被解析为数据、组件的故障、宇宙射线⼲扰芯⽚等…
⽣活中,我们扫描的条形码或⼆维码也是⼀种信息传输的形式,条码上的污垢或划痕都会导致信息错误。
我们⾮常依赖数据正确性,数据不正确可能会产⽣严重的后果,想象⼀下:在线考试的成绩、在线⽀持的⾦额、医学扫描的结果…
于是,⼈们思考:为什么不从传输开始的时候就预防错误的发⽣?
错误检测技术的原理
向数据中添加额外的信息⽤以确认是否发⽣错误。
奇偶校验 Parity Checking
校验规则如下:
举例说明(数据发送⽅)
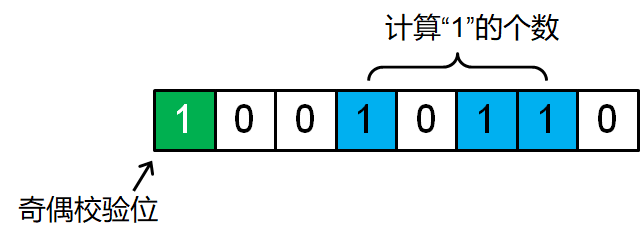
假设要发送⼀段 7bit ⻓度的信息:0010110
1. 在数据⾸位添加⼀个就校验位,记为 X,则数据当前为:X0010110
2. 判断原始数据中有⼏个 1,总共3个,奇数
3. 按照规则,校验位设置为 1,则数据当前为:1010110
4. 发送数据
举例说明(数据接收⽅)
收到了⼀段信息:1010110
1. 通过判断第⼀位奇偶校验位得知数据部分共有奇数个1
2. 判断数据部分是否有奇数个1,3个,奇数,符合校验规则
3. 去掉奇偶校验位,继续后续的数据处理过程
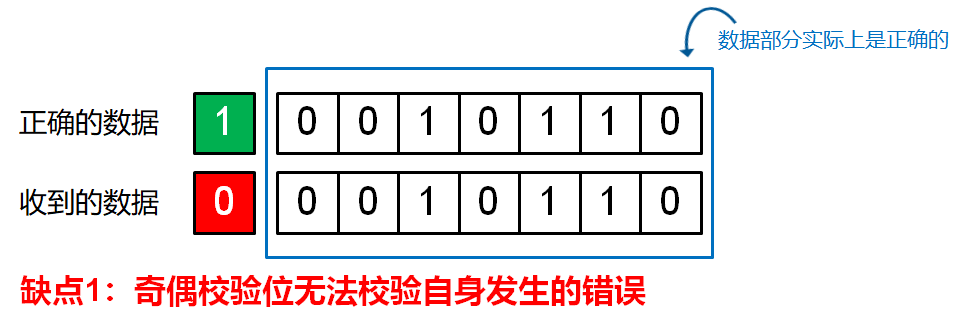
奇偶校验的缺点:校验位翻转
假设在传输过程中,因为不可抗⼒因素导致校验位反转,接收⽅收到的信息如下:
0010110,则判断过程如下:
1. 通过奇偶校验位(0)得知数据部分应有偶数个1
2. 判断数据部分的1的个数,发现有3个,不符合校验规则,丢弃该数据
但实际上,数据部分是正确的。
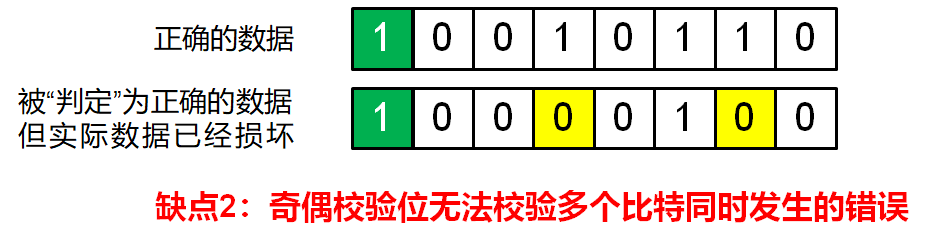
奇偶校验的缺点:多⽐特错误
假设在传输过程中,因为不可抗⼒因素导致数据部分发⽣2个错误,接收⽅收到的信息如下:
10000100,则判断过程如下:
1. 通过奇偶校验位得知数据部分应有奇数个1
2. 判断数据部分1的个数,发现有1个,奇数,符合校验规则
但实际上正确的数据是:10010110
错误检测的游戏



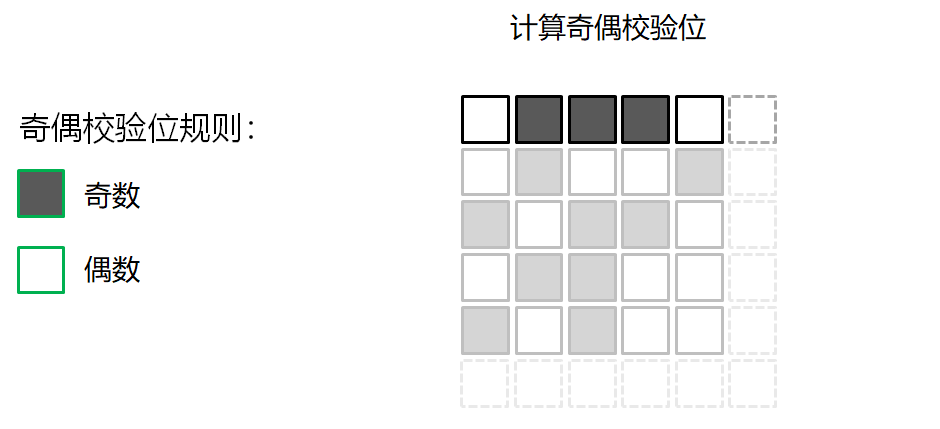
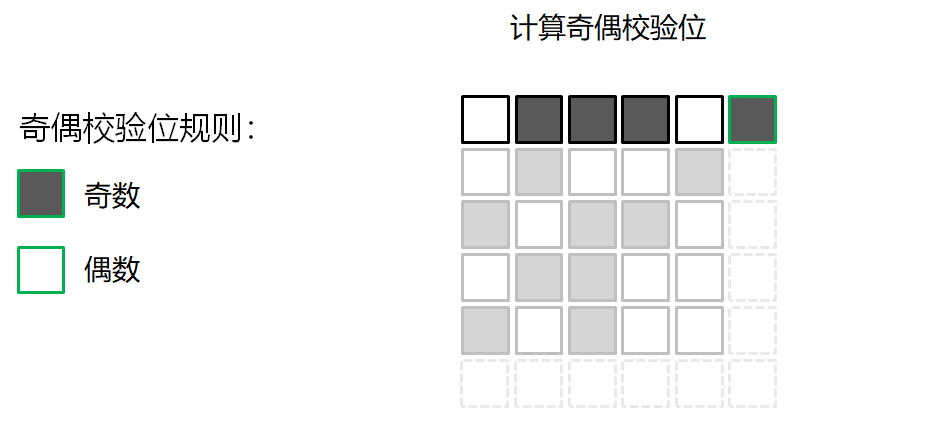
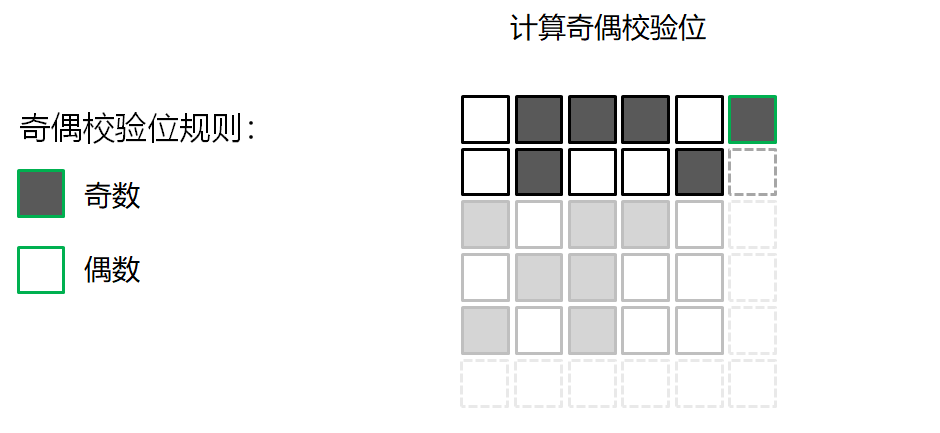
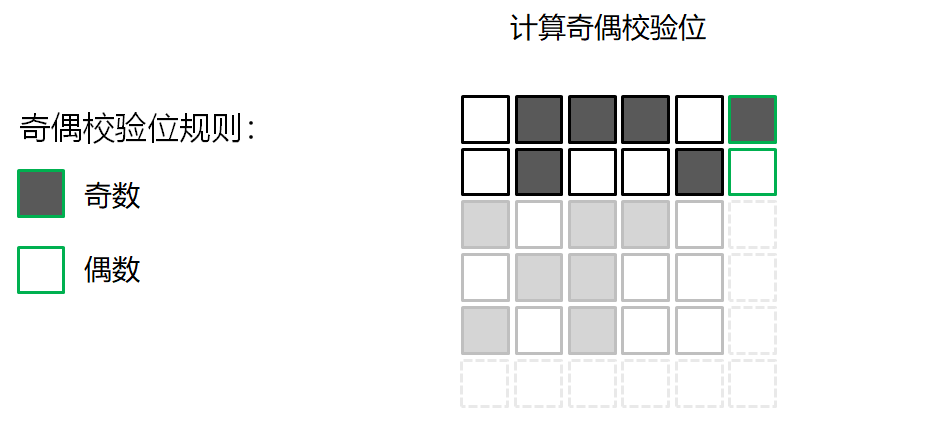
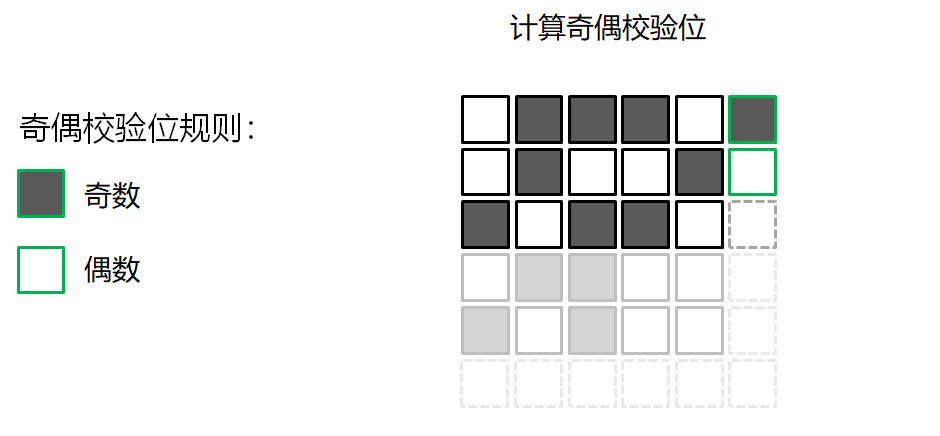
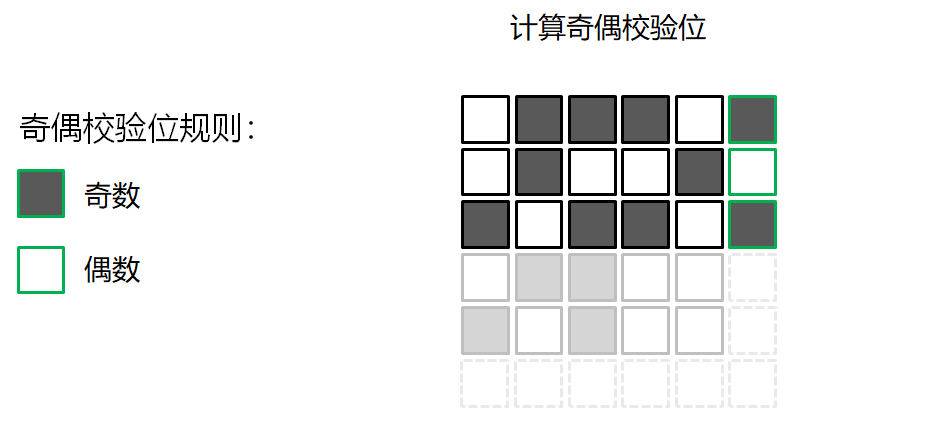
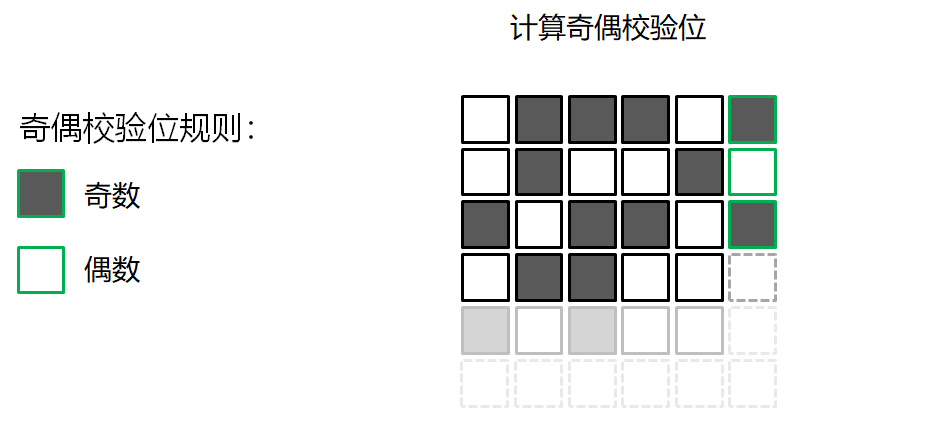
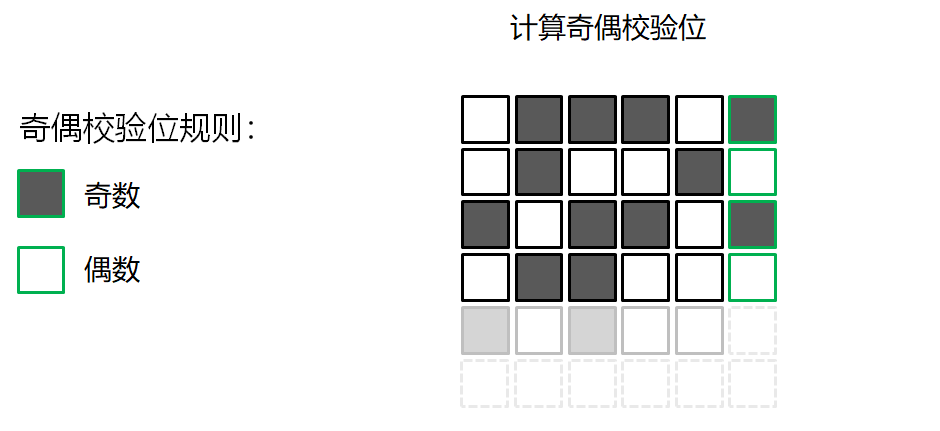
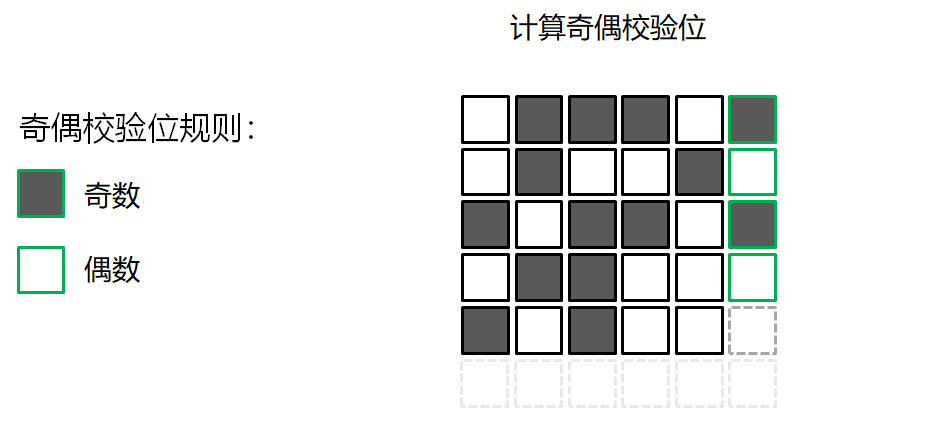
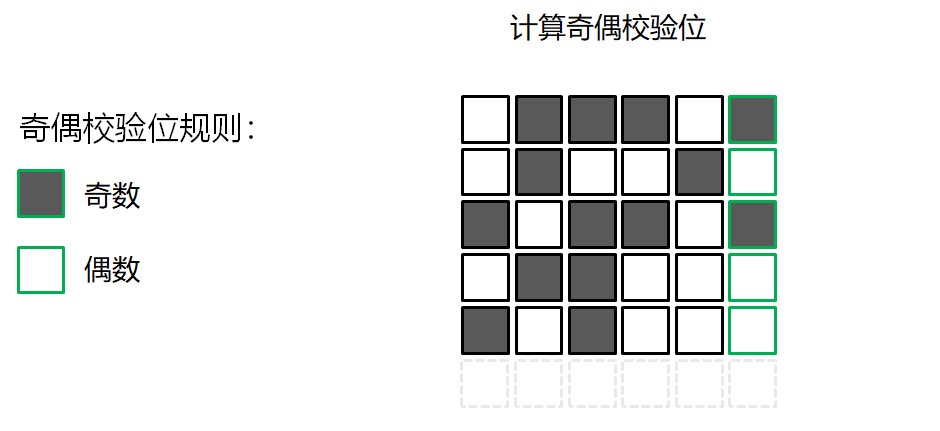
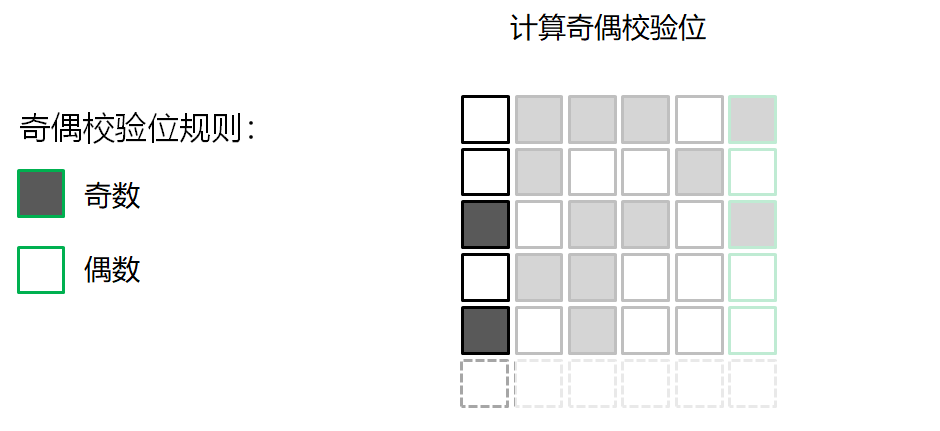
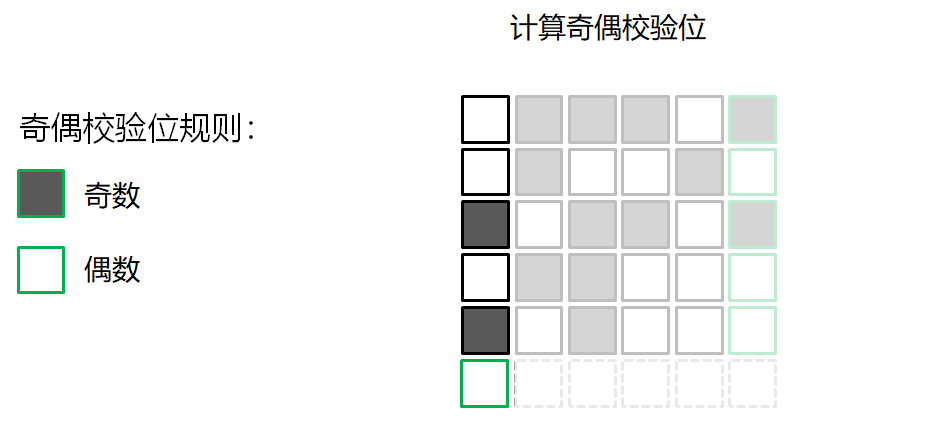

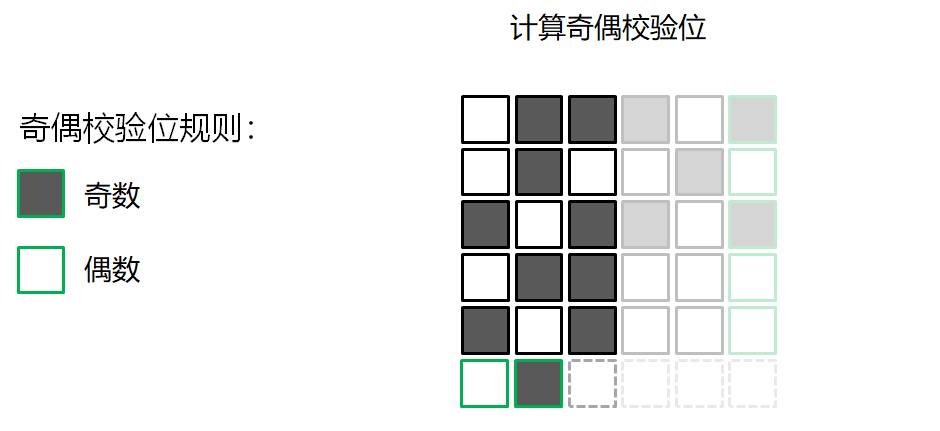
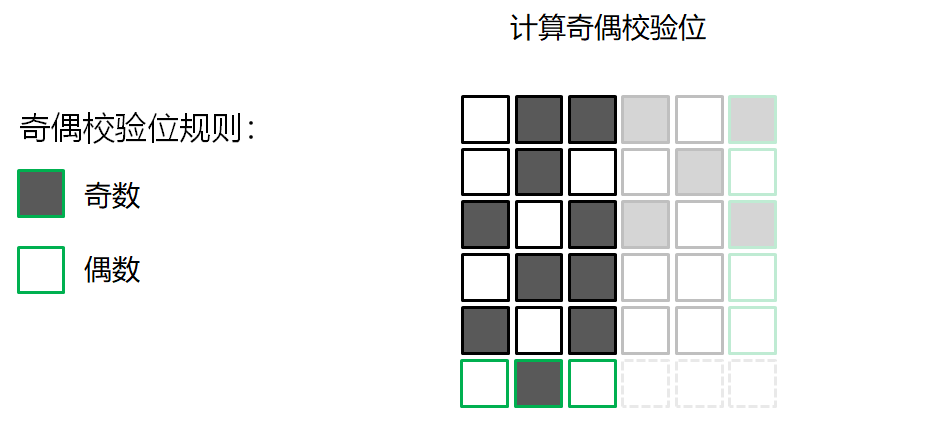
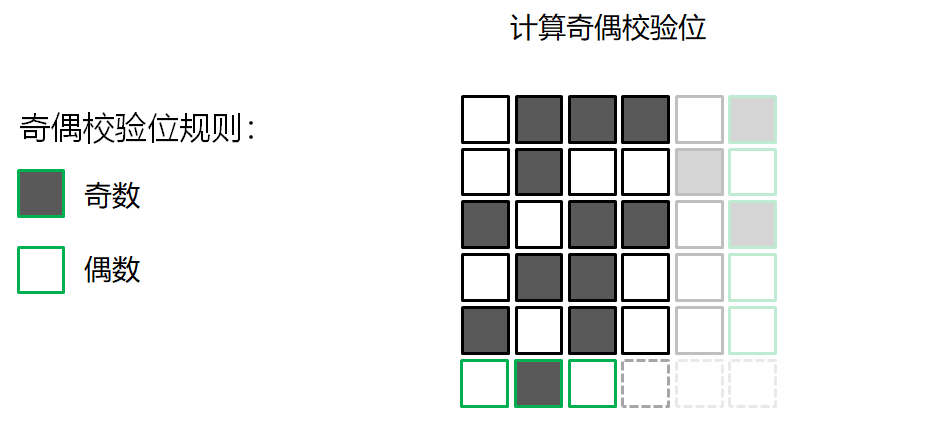
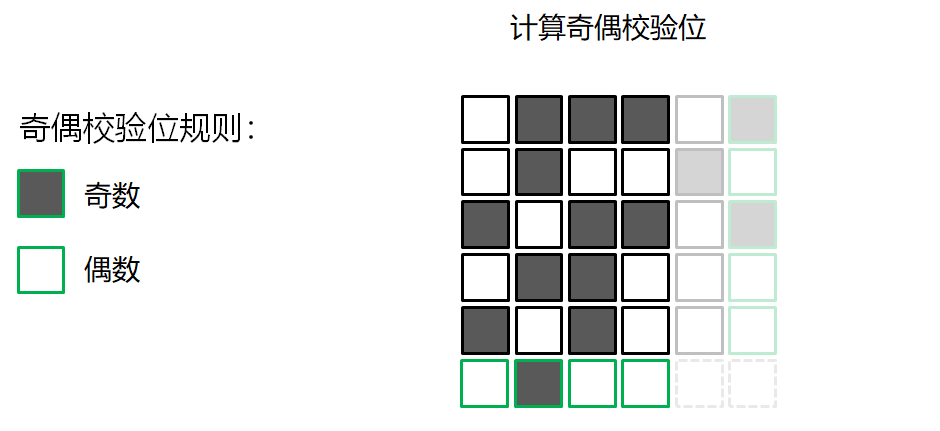
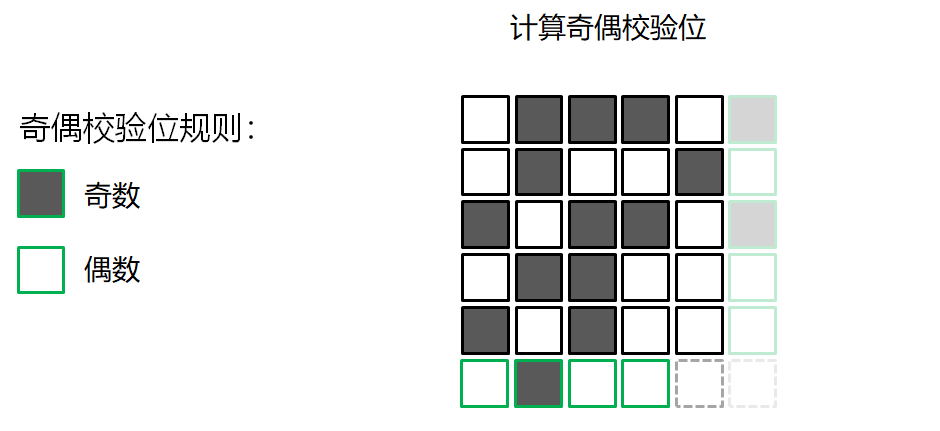

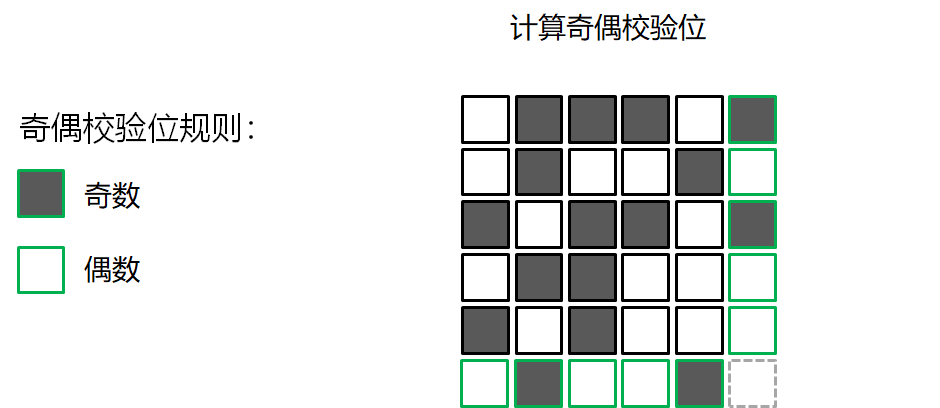
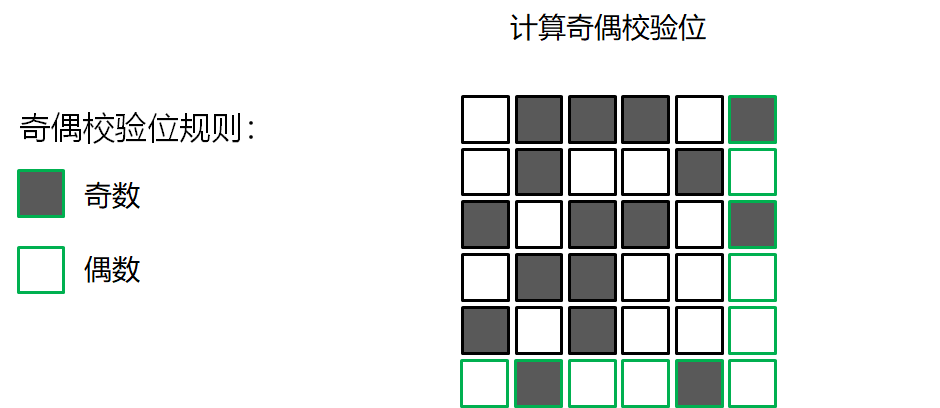
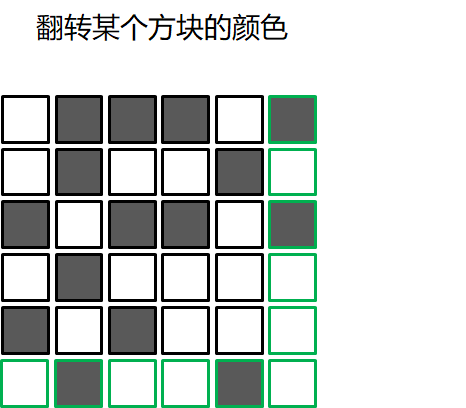



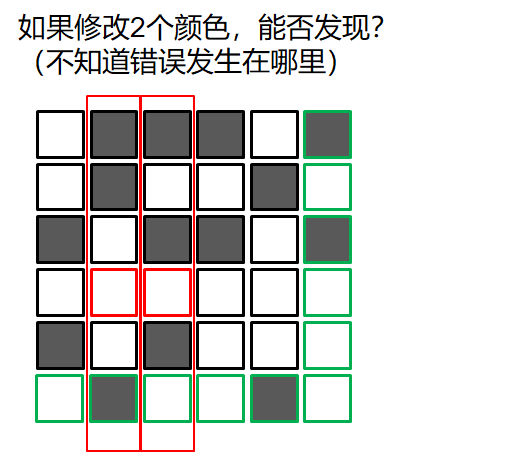

校验和算法 Checksum
奇偶校验就是 checksum 的早期版本形式;通过上⾯的游戏,可以发现单独使⽤奇偶校验聊胜于⽆,它很鸡肋:
如果有 1bit 以上的位发⽣错误,奇偶校验位⽆法发现,发现了也⽆法检测错误
即使奇偶校验位认为正确的数据,也很有可能是因为校验位发⽣了翻转⽽被识别成正确数据
Logic Puzzles
Logic Puzzles 是⼀种根据已知信息排除错误数据的游戏。
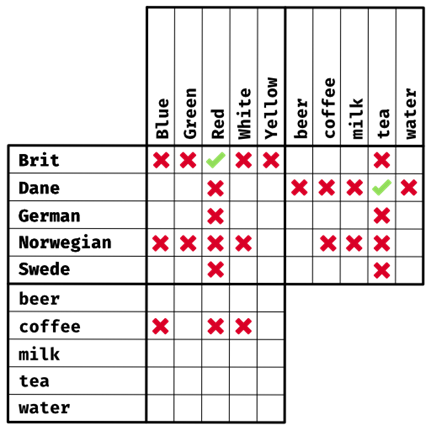
由数学家 Charles Lutwidge Dodgson(查尔斯·卢特维奇·道奇森)制作,他的另⼀个更为⼈所熟知的笔名:Lewis Caroll(刘易斯·卡洛尔),是 《Alice in
Wonderland》爱丽丝梦游仙境的作者。

根据信息,完成以下表格:
有4家新成⽴的交通领域的公司,他们理念各不相同且有不同颜⾊的 logo
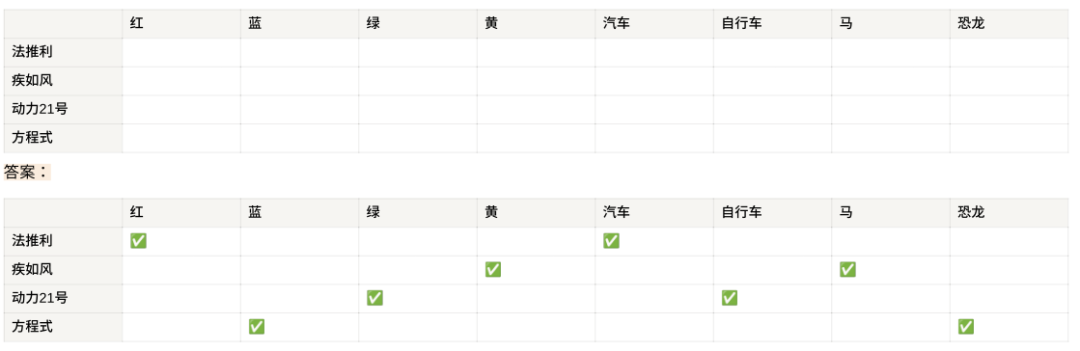
汉明码 Hamming-Code
汉明码是奇偶校验和 Logic Puzzle 的组合,能够检测错误并纠正。
由数学家 Richard Hamming(理查德·汉明)发明。1945年,汉明在洛斯阿拉莫斯为曼哈顿项⽬⼯作,负责编写电脑程序,计算物理学家所提供⽅程的
解。
该程序判断引爆核弹是否会燃烧⼤⽓层,如果不会,则开始实验。

当时,IBM的所有机器都是⽤打孔卡来表⽰和接收数据,汉明必须⾮常严格且认真的检查打孔卡上的数据是否准确。
因为打孔卡会频繁的出现错误:
图:打孔卡,Punched Card
汉明受够了这种情况,他放下了⼿中的⼯作,决定找出⼀种⽅法,能够使计算机可以检测错误并⾃动纠正的⽅法。
汉明码的⼯作原理
汉明意识到,我们⽆需检查信息中每个 bit 的错误,只需要检查某些部分,通过结合各个部分的检查,不仅可以检查错误,还能纠正错误。
下表包含了 16bit 的信息,秘诀在于:表格虽然包含了 16bit 的信息,但实际上真正的数据只有 11bit,其中有 5bit 是奇偶校验位。
这种⽅法很容易扩展,在 16×16 的表格上(256bit),只需要8个奇偶校验位就可以使⽤汉明码
拆解汉明码验证过程
假设你收到了下图表格的数据信息,我们来⼀步⼀步拆解,汉明码的验证过程。
刚刚我们说到,在 16bit 的数据⾥,有 5bit 的奇偶校验位,我们⽤橙⾊背景把它标记出来,为了更加直观的观看验证步骤,将会显⽰⾏号以及列号。
拆解汉明码验证过程
假设你收到了下图表格的数据信息,我们来⼀步⼀步拆解,汉明码的验证过程。
刚刚我们说到,在 16bit 的数据⾥,有 5bit 的奇偶校验位,我们⽤橙⾊背景把它标记出来,为了更加直观的观看验证步骤,将会显⽰⾏号以及列号。
在计算机中,通常⽤0表⽰第⼀个,所以⾏和列都从0开始
Step1.计算奇数列(第1列和第3列)的奇偶校验值,奇偶校验位是第1列的第⼀个数字。需要校验的数据使⽤蓝⾊进⾏标记
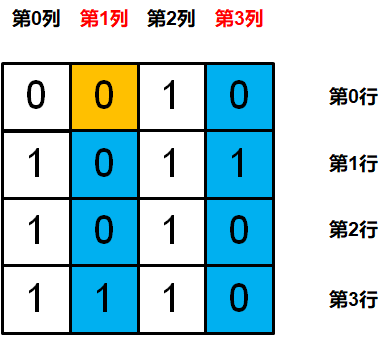
同样使⽤奇偶校验的规则,计算蓝⾊部分有⼏个”1”。总共2个,根据规则,偶数个1,则校验位应为0。
当前奇偶校验位的值为0,说明第1列和第3列数据没有发⽣错误
Step2.计算表格右侧列(第2列和第3列)的奇偶校验值,校验位是第2列的第⼀个数字
校验位错误,说明第2列的数据发⽣错误
Step3.按照相同的⽅式,计算表格奇数⾏(第1⾏和第3⾏)的奇偶校验值,校验位是第1⾏的第⼀个数字。
校验位正确,说明第1⾏和第3⾏没有发⽣错误
Step4.计算表格下半⾏(第2⾏和第3⾏)的奇偶校验值
校验位错误,说明第2⾏发⽣错误
2个错误的奇偶校验位相交的位置(2,2),就是错误发⽣的地⽅(红⾊背景表⽰)
但是如何确定,只有这 1bit 发⽣了错误?诀窍就在于最后⼀个奇偶校验位,在左上⾓(0,0)处。
最后⼀个校验位,会校验全表的数据,但会排除已经出错的 bit
Step5.计算全表的奇偶校验值
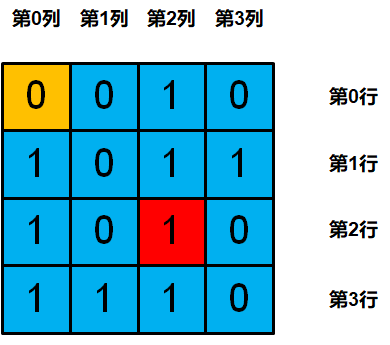
校验正确,说明只有 1bit 发⽣了错误
Step6.修正发⽣错误的 bit
由于⼆进制只有2种状态(0和1)所以只需要翻转⽐特位即可修复错误的数据。
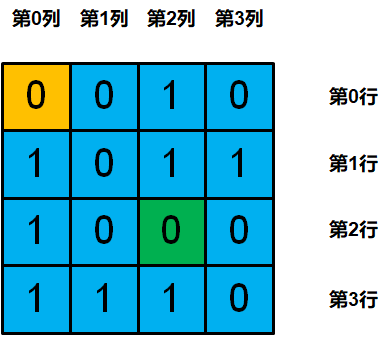
汉明码⽆法检测的情况
汉明码总结
汉明码的优点是⽆需对每⾏每列都添加校验位,⽽是通过“⼀个范围,⼀个区块”来计算奇偶校验值。
汉明码能够检测和纠正单个 bit 的错误,并且可以通过(0,0)处的奇偶校验位检测 2bit 以上的错误,但⽆法修复 2bit 以上的错误,因为不知道错哪⾥了。
但能够知道发⽣了错误,就可以要求重传数据,这是朝着正确的⽅向迈了⼀⼤步
RAID 5 与汉明码
汉明码检查⾏和列的⽅式类似于 RAID 的条带化(striping)技术。
以 RAID5 为例,⾄少需要3块磁盘,并提供奇偶校验的条带,数据被切分成“块”(每2个数据块就有1个奇偶校验块)分布在多个磁盘上,如果⼀块磁盘发
⽣故障,丢失的数据可以从其他磁盘上进⾏重建。
与汉明码相同,RAID5 最多⽀持⼀块磁盘发⽣故障。
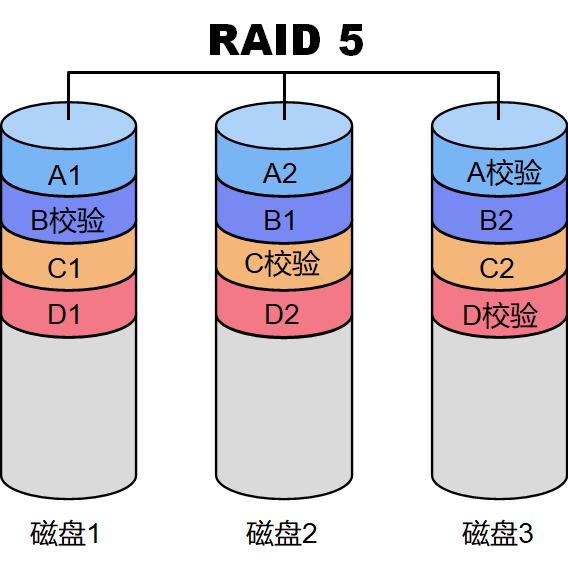
⾥德·所罗门编码 The Reed-Solomon Code
在汉明码发明后的10年,Gustave Solomon(古斯塔夫·所罗门) 和 Lriving Reed(欧⽂·⾥德) 发表了他们⾃⼰的论⽂《Polynomial Codes over Certain FiniteFields》译: 有限域上的多项式编码。

该论⽂描述了⾥德所罗门码,⽤于许多数据存储的技术、以及许多数据传输技术的纠错码。
多项式插值(Polynomial interpolation)
⾥德所罗门算法将数据列表⽰为多项式上的点,通过图上的其他点来作为奇偶校验的数据。
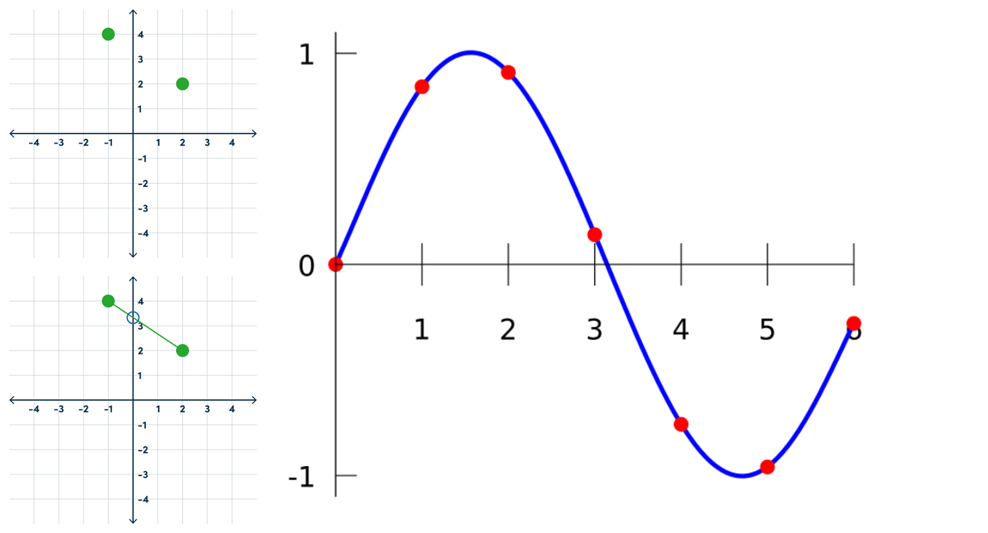
伽罗⽡域(Galois Field)
由法国数学家 Evariste Galois(埃⽡⾥斯特·伽罗⽡)提出,在数学中,有限域是包含有限个数的域,是⼀个封闭的世界,⾥⾯有限个数字不管怎么计算,都
不会得到它们之外的结果。
伽罗⽡,17岁时已发表多篇论⽂,因考官⽆法理解他的思路,申请⼤学被拒,不仅热衷数学,还热衷政治,该与批评。
⽣命最终定格在20岁。
举例: GF(2^3)=0,1,2,3,4,5,6,7
伽罗⽡域中的加法和减法,使⽤异或计算
伽罗⽡域中的乘法和除法,使⽤模⼆乘法
⾥德所罗门编码的应⽤
播放有轻微划痕的DVD
条形码(也叫⼀维码)和⼆维码
数据存储技术 RAID 6
Voyager2 旅⾏者2号探索太阳系任务

分布式存储 Ceph 也使⽤纠删码确保数据可靠性
纠删码能够允许 Ceph 复制你的数据⽽不做完整副本,⽽是从碎⽚中重建数据。这些碎⽚分布在多个磁盘驱动器。提供了极⾼的数据耐久性,同时保证了
存储容量处于极低的状态。
⼏乎所有的 Ceph 中的纠删码都依赖于某种形式的⾥德所罗门编码,只不过每种算法各有各的优势,不同算法基本区别就是:如何进⾏矩阵计算。
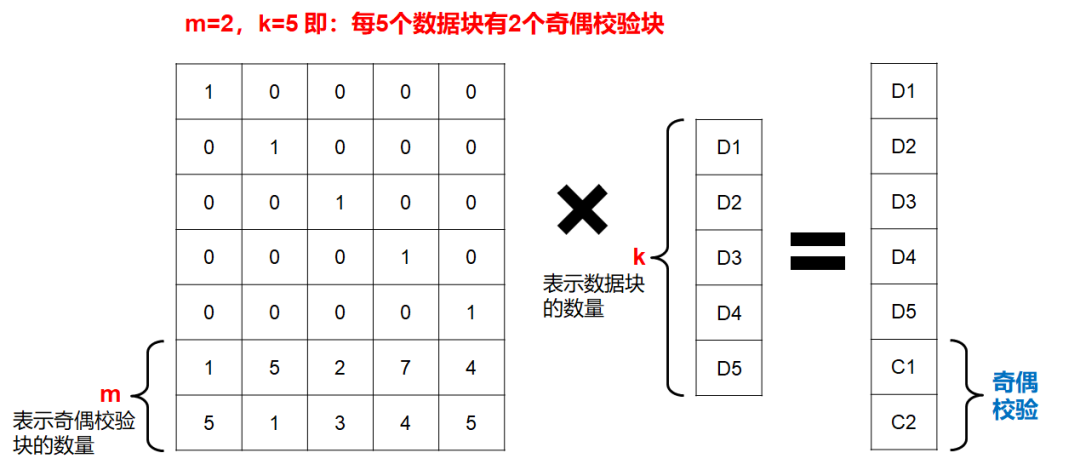
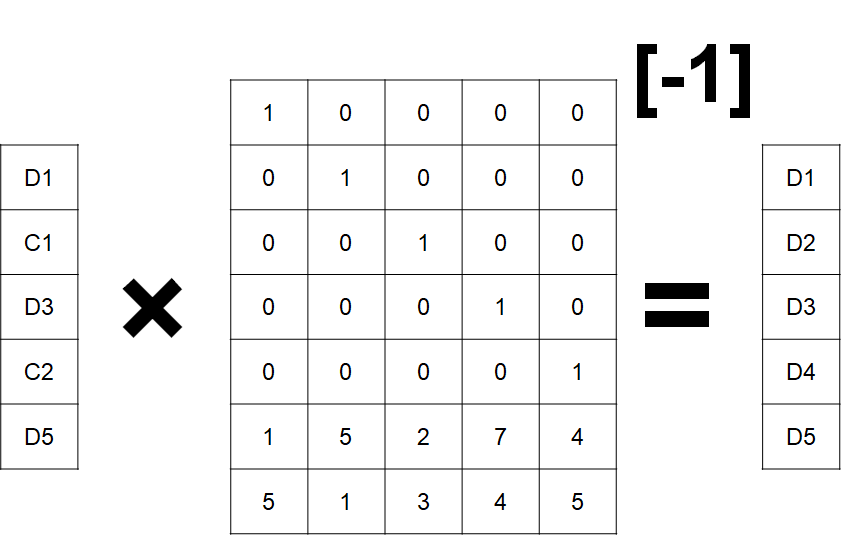
RAID 6 与⾥德所罗门编码
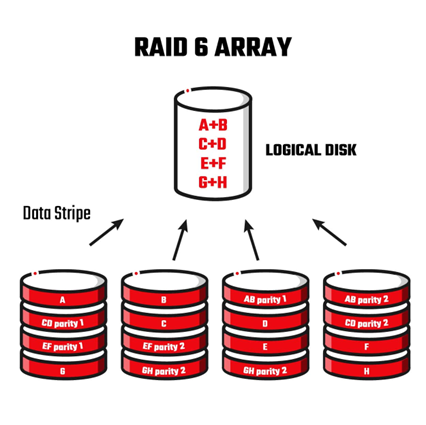
RAID6 同样基于“⾥德所罗门编码”,所以⽀持同时损坏2块磁盘,相⽐基于汉明码的 RAID5 ⼤⼤提⾼了容错性。
常⻅的 RAID6 术语

PD 盘即:Parity Drive 奇偶校验盘。在⽩⽪书中被称为 P盘,包含 XOR 数据,由所有数据盘⽣成。
RS 盘即:Reed-Solomon 在⽩⽪书中被称为 Q盘,也是由所有数据盘⽣成⽽来
只要PD盘和RS盘存在,整个磁盘阵列最多可以损失2个数据盘
RAID6 中的7种硬盘损坏情况

使⽤ Python 验证 RAID5/6
环境 CentOS 7.9
Python版本 3.6.8
1.设定3块盘的初始数据

2.⽣成PD盘的奇偶校验数据
创建⽂件 xor_data.py ⽤于⽣成奇偶校验盘数据


运⾏ xor_data.py 查看效果

PD盘的初始数据如下
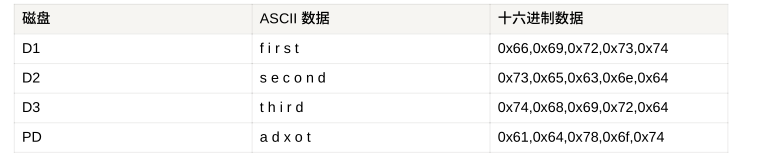
假设此时数据盘D3损坏(RAID5 恢复原理)
创建⽂件 raid5_example.py ⽤于模拟⼀块盘损坏并恢复

执⾏ raid5_example.py 并对⽐输出结果是否和原先D3数据⼀致

3.⽣成伽罗⽡域
创建⽂件 gflog_tables.py ⽤于⽣成伽罗⽡域


4.定义伽罗⽡域的操作
创建⽂件 rs_functions.py ⽤于定义加法、乘法、除法

5.⽣成 RS 盘的纠删码
创建⽂件 recover_rs.py ⽤于⽣成纠删码
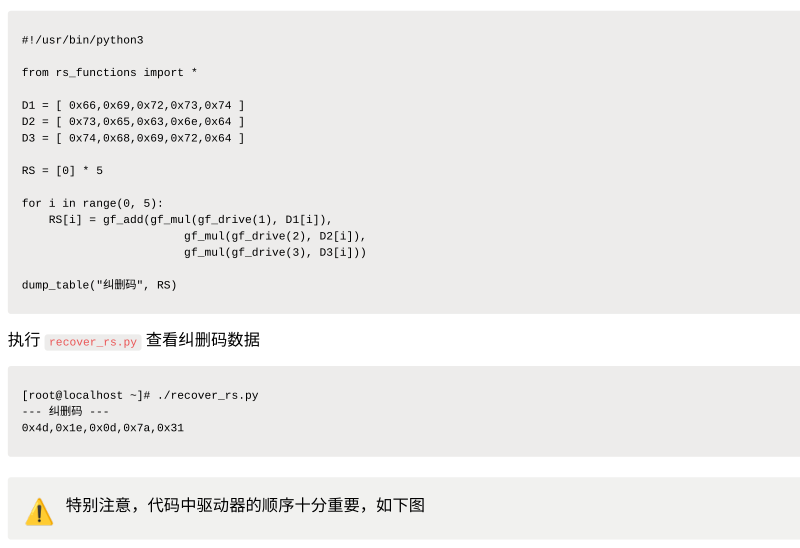
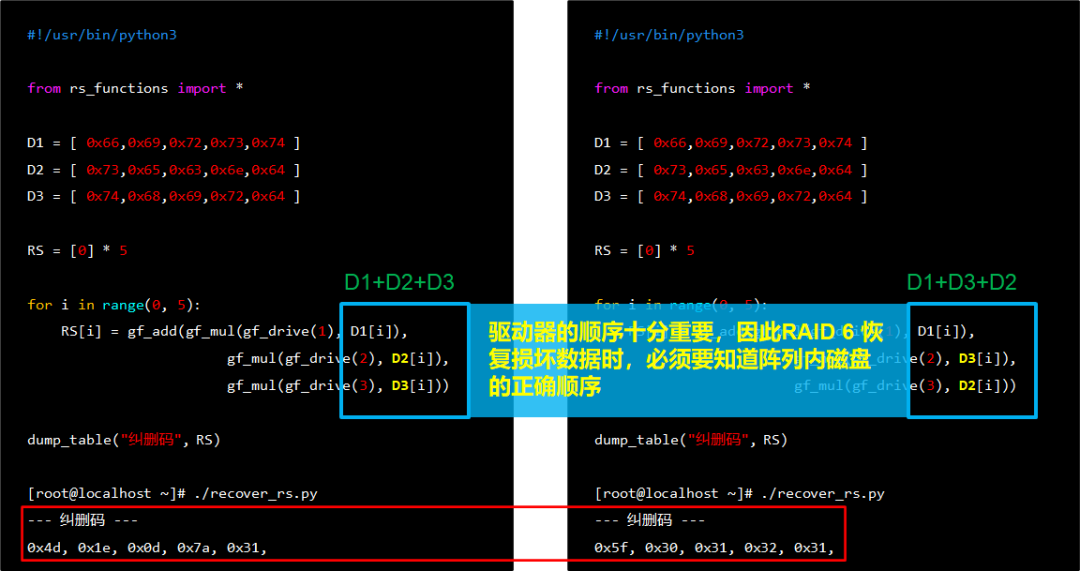
6.五块盘的初始数据⽣成完毕

演⽰磁盘损坏后还原数据
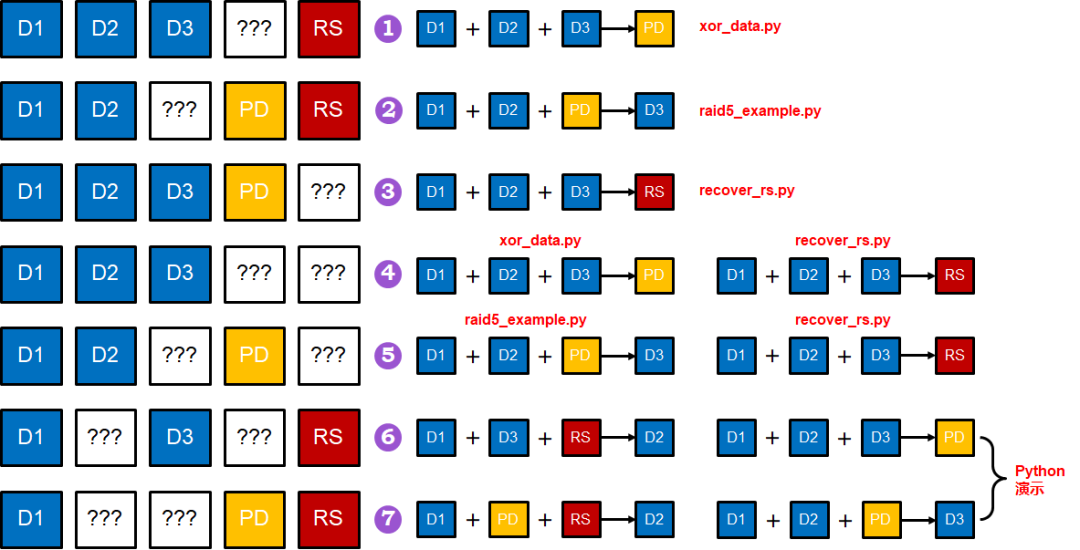
同时损坏1块数据盘和1块PD盘
创建⽂件 recover_d2_and_pd.py ⽤于模拟情况
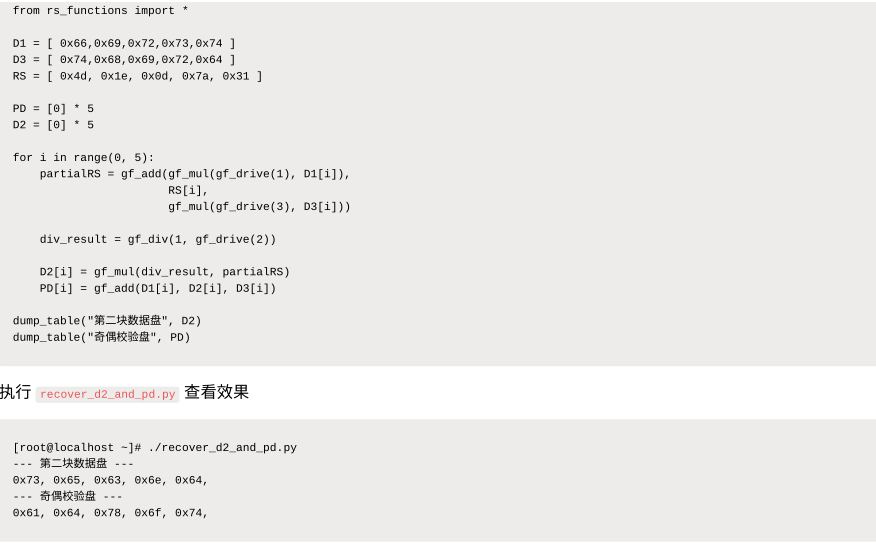
同时损坏两块数据盘
创建⽂件 recover_d2_and_d3.py ⽤于模拟两块磁盘损坏


end
—年度热文 —







系统集成
认证培训
买设备,找我们
IT维保,找我们
IT培训,找我们
限时特惠:本站每日持续更新5-20节内部创业项目课程,一年会员
只需199元,全站资源免费下载点击查看详情
站长微信:
jjs406





