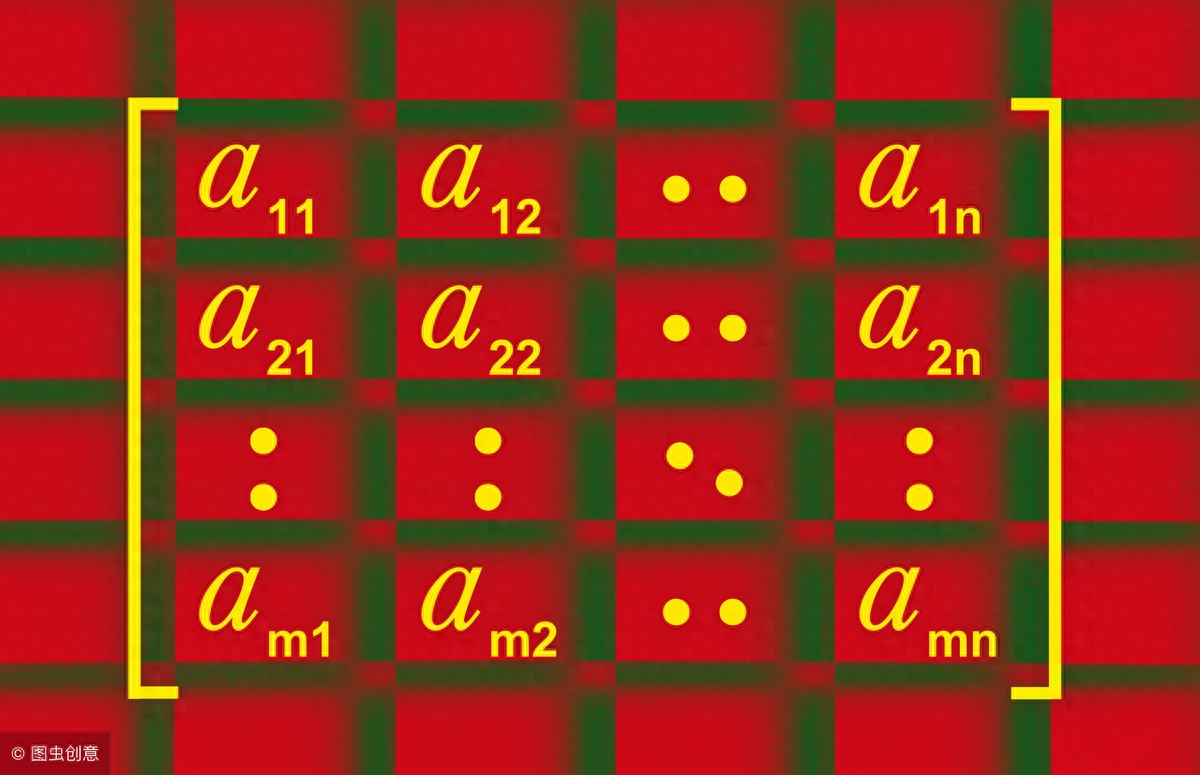
我们在前三讲中主要讲了如下内容:
向量:就是一组量,水平排列就是行向量,竖直排列就是列向量。
我们规定了向量的内积或者数积:就是向量对位的乘积和。以此我们可以刻画向量的模,就是相同向量的内积再开根号。而向量的指向通过射影的概念,用两个向量的内积比两个向量的模来加以反映。两个向量的平行与正交也进行了定义。
矩阵:就是以列向量水平排列的行向量,反之也行。我们定义了幺阵,定义了矩阵的转置,矩阵的加减乘法,定义了矩阵的转置与矩阵的逆,这就建立了矩阵的基本运算规则。
对于向量,可以有平行关系,一般来说关系可以有相关与无关,相关的意思是:如果n个向量,其中一个向量可以用另外的向量线性组合表达出来,这n组向量就是相关的,反之是无关的。
N维空间就是指,给定n个相互独立的向量,其线性组合形成的所有向量构成一个n维向量集合,空间上可以定义向量的运算。这n个独立的向量叫做该空间的基底,空间是基底扩张形成的集合。
n维向量空间的基底如果相互正交,则表达线性空间的向量会比较方便,这涉及矩阵的正交化问题,我们后续会讲如何做。
注意到我们所涉及的内容大部分是从几何出发引申出来的,长度与方向已经有了很好的表达,但面积体积这样的概念却并没有包含在内。这涉及到向量的另外一种乘法:外积。本讲先回到线性代数的起点:解线性方程,我们讲行列式,行列式可以看成方形矩阵的自运算,用于实现矩阵值的量,国外多用determination这词来表达其与矩阵的关系。
二阶与三阶行列式
定义:矩阵的行列式对应着一个方矩阵的值,设A是个n元矩阵,
就是这个矩阵的行列式值。下面我们将利用矩阵与行列式的概念重新看看一次方程的解。
二元一次方程组可以写成
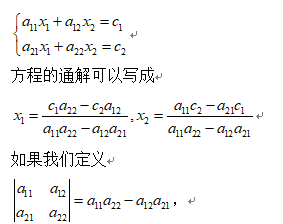
并叫这个式子是二阶行列式的话,那么方程的解可以写成:
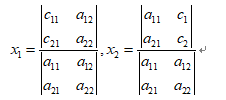
方程组有解的条件也变为
上面的做法没有特别的新意思,就是把代数运算整理成了一规整的的形式。
类似地对三元一次方程组
来说解方程的过程如下,我们先不要怕麻烦,要通过代数运算找出规律来。
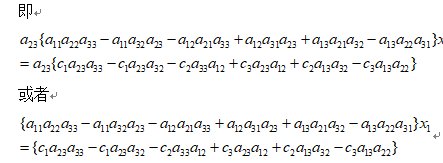
方程有解的条件为:
注意到

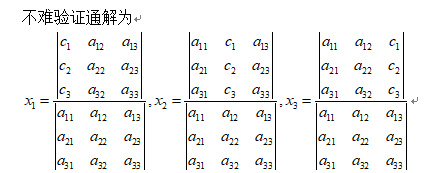
也是非常规整的。
一般行列式的定义
矩阵的行列式对应着一个方矩阵的值,设A是个n元矩阵,det(A)就是这个矩阵的行列式值。
其中:
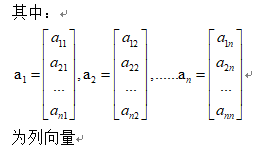
我们已经知道二阶,三阶行列式的计算方法了。四阶行列式的算法可以写成:
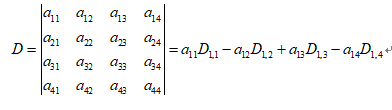
上式中D代表n阶行列式,Dij代表删去i行j列后剩下的n-1阶行列式,也叫余子式.
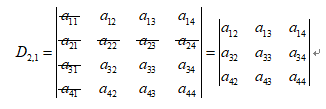
我们可以对n阶行列式做递归定义:即由n-1阶行列式描述n阶行列式
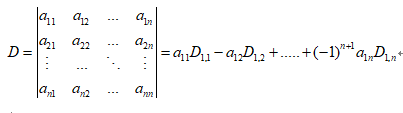
对二三阶行列式而言有
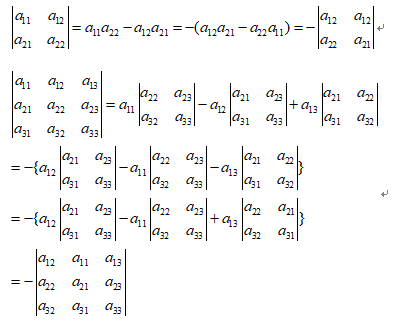
即任意的两行或者两列相互置换所得新的行列式差一个负号。下面我们来论证对于任意阶的行列式都有这样的性质。
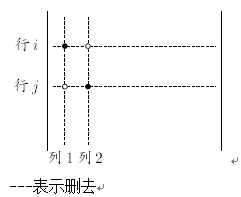
令Dij,12表示一个行列式中删去,i,j行,1,2列后剩余的行列式。
实际操作时,可以有两种方式获得Dij,12
.对Di,1删掉其中对应于D的j行与2列
. Dj,2删掉对应于D的i行与1列


将上面的1或者2用任意小于n的整数k加以替换,推导依然正确,再考虑到
推论1
行列式D中任意两列或者任意两行的交换后得到的新行列式是原来行列式的相反数,也就是说做行或者列交换,行列式值变号。
证明:列1i,1j,j1
则1复原,i,j交换,依次考虑计算D的过程,三种情况D的符号变了3次,所以D变号。
推论2
如果行列式中两行或者两列相同,则行列式的值为0。
对下面的n元方程
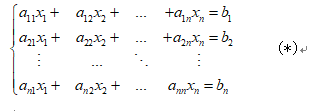
系数矩阵可以写成
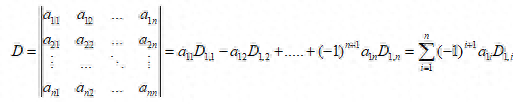
对n元方程(*)的每个方程施以运算
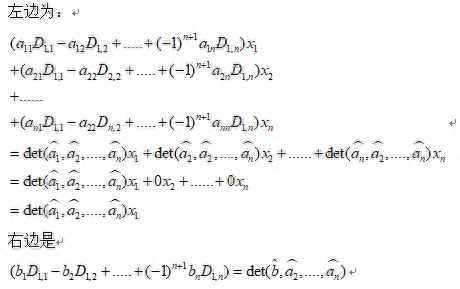
右边是
所以n元方程有解的条件为系数行列式的值不为0,解方程的问题就变成了算行列式的问题。这就是解线性方程组的主要理论。
有了这四讲垫底,想深入学习的可以找大学线性代数教材自学了,最好找欧美法风格的入门级线代课本。网络上流传很广的一个视频是可汗学院出品的一个可视化从物理,数学,信息科学的角度来看矩阵的,国内洗稿者不计其数,至少头条就有几篇高点击率的。站位并不高,只是国内高中与大学线性代数缺乏衔接,所以大学生特别是一般的大学生觉得线性代数很抽象,很无用而已。
这四讲仔细读过,再结合研究生考纲,研究生入学考试的线性代数的基本基础也就有了。教育要革命,学制要缩短,我信这个,呵呵。
限时特惠:本站每日持续更新5-20节内部创业项目课程,一年会员
只需199元,全站资源免费下载点击查看详情
站长微信:
jjs406





