第一章
1. 统计学:研究数据的搜集、整理与分析的科学,面对不确定性数据作出科学的推断。因而统计学是认识世界的重要手段。
2. 食品试验设计与统计分析:数理统计原理与方法在食品科学研究中的应用,是一门应用数学。
3. 食品试验科学的特点:1.食品原料的广泛性 2.生产工艺的多样性 3.质量控制的重要性 4.不同学科的综合性
4. 统计学发展概貌:古典记录统计学、近代描述统计学、现代推断统计学。
第二章
5. 总体:根据研究目的确定的研究对象的全体。
6. 个体:总体中一个独立的研究单位。
7. 样本:根据一定方法从总体中抽取部分个体组成的集合。
8. 样本含量n(样本容量):即样本中个体的数目。(n≤30的样本叫小样本,n≥30的样本叫大样本)
9. 随机样本:总体中的每一个个体都有同等机会被抽取组成样本。
10. 参数:由总体计算的特征数。
11. 统计量:由样本计算的特征数。
12. 参数和统计量的关系:由相应的统计量来估计参数,如样本平均数估计总体平均数,样本标准差估计总体标准差。
13. 准确性(准确度):在调查或试验中某一实验指标或性状的观测值与真实值接近的程度。(观测值与真实值之间)
14. 精确性(精确度):在调查或试验中同一实验指标或性状的重复观测值彼此接近的程度。(观测值与观测值之间)
15. 试样中的误差:随机误差和系统误差。
16. 随机误差(抽样误差):由许多无法控制的内在和外在偶然因素所造成的误差,不可避免和消除,影响试验的精确性。
17. 系统误差(片面误差):由于试验对象相差较大,测量的仪器不准、标准试剂未经校正所引起,可以通过改进方法、正确试验设计来避免、消除,影响试验准确性。
18. 资料的分类:连续性资料:对每个观测值单位使用仪器或试剂等量测手段来测定其某项指标的数值大小而得到 的资料。
间断性资料:用计数方式得到的数据资料。
分类资料:可自然或人为地分为两个或多个不同类别的资料。
等级资料:将观察单位按所考察的性状或指标的等级顺序分组,然后清点各组观察单位的次数而得的资料。
19. 连续性资料的整理:采用组距式分组
1.求全距 2.确定组数 3.求组距 4.确定组限和组中值(最小值为下限,最大值为上限。第一组的组中值以接近于或等于资料中最小值为好。)5.制作次数分布表
20. 统计表的绘制原则:结构简单,层次分明,内容安排合理,重点突出,数据准确,便于理解和分析
21. 统计表种类:简单表,复合表
22. 统计图:用图形将统计资料形象化。长条图、圆图、线图、直方图、折线图。
23. 平均数`X:指出资料中数据集中较多的中心位置,描述资料的集中性。反应了总体分布的集中趋势。
24. 平均数的种类:算术平均数、中数、众数、几何平均数、调和平均数。
25. 算数平均数计算方法:直接法、加权法
26. 算数平均数的特性:离均差为0,离均差平方和最小。
27. 离均差:每个观测值均有一个偏离平均数的度量指标。算术平均数的离均差之和为零。
28. 离均差平方和:各个离均差平方后相加。
29. 方差(MS):也称均方,各数据与平均数的差的平方和与自由度的比。样本方差用S2表示。(无单位)
30. 自由度df:样本内独立而能自由变动的离均差个数。
31. 标准差:样本方差的算术平方根。(有单位,与观测值单位相同)
32. 标准差的特性: 1.标准差的大小受每个观测值的影响,若数值之间变异大,其离均差亦大,标准差必然大。
33.
2.各观测值加或减同一常数,标准差的值不变。
3.每个观测值乘以或除以一个不等于0的常数A时,所得标准差是原标准差的A倍或1/A。
34. 样本标准差:EXCEL用STDEV函数计算。
35. 变异系数CV:标准差相对于平均数的百分数。反映了总体的可比程度。
CV=
36. 变异系数的作用:当资料所带的单位不同或单位虽然相同而平均数相差较大时,不能直接用标准差比较各个样本资料的变异程度大小。消除了不同单位和平均数的影响。
第三章
37. 伯努利试验:只有两种实验结果的随机试验。
38. N重伯努利试验:伯努利试验在完全相同的实验条件下独立的重复n次,并作为一个随机试验。
39. 二项分布x~B(n,p):离散型随机变量分布。
P(x=k)=
(k=0,1,2,3…,n)
40. 二项分布的特征
1.Pn(K)≥0 2.(p+q)n=1 3.在一定范围内的总概率P等于被包含的几个概率之和。
4.当p值较小且n不大时,分布是偏倚的。随着n的增大,分布逐渐趋于对称。
5.当p值趋于0.5时,分布趋于对称。
41. 二项分布的应用条件:
(1)试验结果为两大类或两种可能的结果。
(2)每次试验的条件不变,每次试验A的发生概率均为π。
(3)各次试验独立,每个观察单位的观察结果不会影响到其他观察单位的结果。
42. 二项分布的平均数:m=np
43. 二项分布的方差:s2=npq
44. 泊松分布x~P(l):可以用来描述和分析随机地发生在单位空间或时间里的稀有事件的分布。(即小概率事件分布,意外事故、自然灾害都近似服从)
P(x=k)=
45. 泊松分布特点:离散型随机变量概率分布,均值与方差相等。μ=σ2=λ。
46. 泊松分布的应用条件:
1. 随机地发生在单位时间或空间里的稀有事件的概念分布。
2. 在二项分布中,n很大,p很小时。
3. 事件不随机时,不能用泊松分布。
47. 正态分布x~N(m,s2):连续型随机变量的概率分布。
48. 正态分布的特点:
1. 正态分布曲线是以均数m为中心左右对称的单峰悬钟形曲线。在平均数的左右两侧,只要(x-m)绝对值相等,f(x)值就相等。
2. f(x)在x=m处达到最大值,且f(m)=1/(σ
3. f(x)是非负函数,以横轴为渐近线,分布从-∞到+∞,且曲线在m±σ处各有一个拐点。
4. m是位置参数,σ2是形状参数。
5. 正态分布的次数多数集中于平均数m的附近,离均数越远,其相应的次数越少。
6. 曲线f(x)与横轴之间所围成的面积等于1。
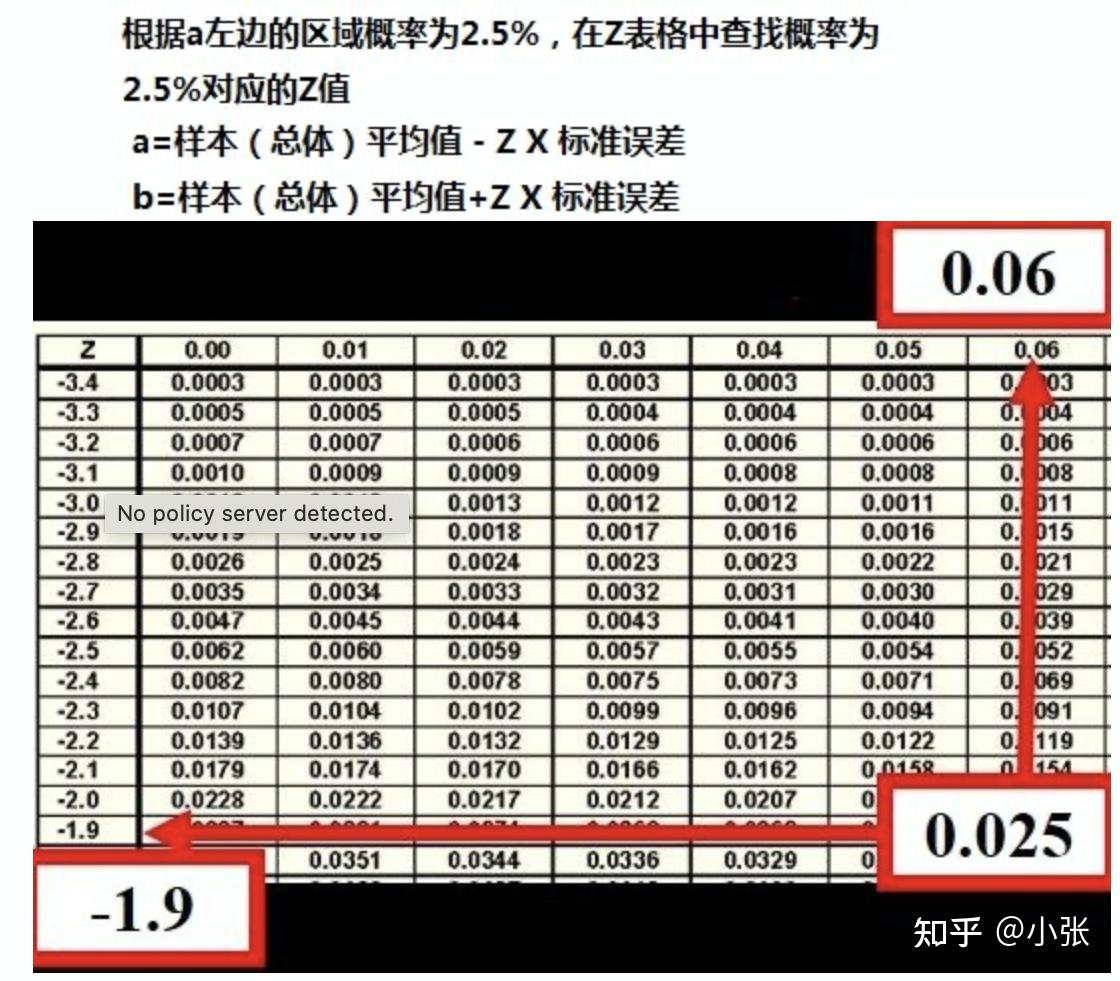
49. 标准正态分布u~N(0,1):m=0,σ2=1的正态分布。
50. 标准正态变量(标准正态离差)u:u=(x-m)/σ
51. 三种分布的关系:
1. 二项分布,当n很大,np、n(1-p)接近,该分布接近于正态分布。
2. 在n®∞、p®0.5时或p>0.1时可用二项分布代替正态分布。
3. 当n®∞、p®0,且np=l(较小常数)时,用泊松分布代替二项分布。
4. 当p<0.1且n很大时,用泊松分布代替二项分布。
5. 泊松分布,l≥30时,用正态分布代替。
52. 抽样分布:统计量的分布概率。
53. 抽样误差:由随机抽样造成的误差。
54. 标准误差(标准误,均数标准误):样本平均数抽样总体的标准差。反应精确性的高低,s`x越大精确度越低。
55. t分布:在计算S`x时,由于采用S来代替s,使得t变量不再服从标准正态分布,而是服从t分布。
t=(`x-m)/S`x
第四章
56. 统计推断:根据抽样分布规律和概率理论,由样本结果去推断总体特征。主要包括假设检验(显著性检验)和参数估计。
57. 表面效应:样本平均数与总体平均数的差异。包含两总体平均数的差异(处理效应)(m-m0)和试验误差`e。
`x-m0=m+`e-m0=(m-m0)+`e
58. 统计假设检验:对研究总体提出假设,然后在此假设下构造合适的检验统计量,并由该统计量的抽样分布计算出样本统计量的概率,再根据概率值的大小作出接受或否定假设的判断。
59. 无效假设H0:通过检验,可能被接受,也可能被否定。
60. 备择假设HA:与无效假设相对应的假设。
61. 进行假设检验的基本依据:把小概率事件在一次试验中看成是实际不可能发生的事件称为小概率事件实际不可能性原理。
62. 显著水平a:决定接受或否定H0的小概率标准。(常用显著水平有0.05和0.01)
63. 统计假设检验步骤:1.建立假设 2.确定显著水平α 3.检验计算 4.统计推断
64. Ⅰ型错误(第一类错误):指当H0本身正确,但通过假设检验后却否定了它,也就是将非真实差异错判为真实差异。犯第一类错误的概率是a。(减少Ⅰ型错误,可将显著水平定得小一点。)
65. Ⅱ型错误(第二类错误):当H0本身错误时,通过假设检验后却接受了它,也即把真实差异错判为非真实差异。(减少Ⅱ型错误,通常是通过减少均数标准误来减小第二类错误的概率。而均数标准误的减小是通过精密的试验设计、严格的试验操作和增大样本容量来实现的。由于一般来说α大β就小,增大了犯第一类错误的概率时,犯第二类错误的可能性就小。反之,α小,β大。因此在实践中可以根据试验目的,通过调整α的大小来控制检验时犯错误的概率。)
66. 两尾检验:备择假设中,包含了μμ0两种情况,因而这种检验有两个否定域,分别位于样本平均数分布曲线的两尾。
67. 一尾检验:否定域位于`x分布曲线某一尾的统计假设检验。
68. 选用两尾检验还是一尾检验应根据专业的要求在试验设计时确定。若事先不知道μ与μ0谁大谁小,为了检验两者是否有差异就用两尾检验。如果能凭借专业只是推测μ不会小于(或大于)μ0时,为了检验μ是否大于(或小于)μ0应用一尾检验。
69. u检验:在假设检验中利用标准正态分布来进行统计量的概率计算的检验方法。
70. u检验使用范围:若样本资料总体方差已知,或样本含量≥30时用u检验。
71. 假设统计误差中试验误差:随机误差
72.
统计假设检验中应注意的问题:1.试验要科学设计和正确实施 2.选用正确的统计假设检验方法 3.正确理解差异显著性的统计意义 4.合理建设统计假设,正确计算检验统计量
单个样本平均数的假设检验
1) 单个样本平均数的u检验:
某罐头厂生产肉类罐头,其自动装罐机在正常工作时每罐净重服从正态分布N(500,64)(单位,g)。某日随机抽查10瓶罐头,测其净重见表。分析装罐机当日工作是否正常?
编号
10
净重(g)
505
512
497
493
508
515
502
495
490
510
2) 单个样本平均数的t检验:
t检验:在假设检验中利用t分布来进行统计量的概率计算的检验方法。
两个样本平均数的假设检验:由两个样本平均数之差,去判断这两个样本所在的总体平均数有无显著差异。
一、 成组资料平均数的假设检验:
1) U检验
1、 如果两个样本资料都服从正态分布,且总体方差
和
已知。
2、 总体方差未知,但两个样本都是大样本时,平均数差数的分布呈正态分布。
2)
t检验
1.
如果两个样本资料都服从正态分布,且=时,不论是大样本还是小样本,都有下式服从具有自由度df=n1+n2-2的t分布:。
二、
成对资料平均数的假设检验:
73. 二项百分率的假设检验
1)
单个二项百分率的假设检验
2) 单个二项百分率的假设检验
第五章
74. 方差分析(变量分析):关于观测值变异原因的数量分析。(三个或三个以上水平的分析,小于3个用t检验。)
75. 试验设计的作用: 1.可以分析清楚试验因素对试验指标影响的大小顺序,找出主要因素,抓住主要矛盾 2.可以了解试验因素对试验指标影响的规律性 3.可以了解试验因素之间相互影响的情况 4.可较快地找出优化的生产条件或工艺条件,确定优化方案 5.可以正确估计、预测和有效控制、降低试验误差,提高试验精度 6.可以明确为寻找更优生产或工艺条件、深入揭示事物内在规律而进一步研究的方向。
76. 试验指标:根据研究目的而选定的用来衡量或考核试验效果的质量特性。如:考察加热对果胶酶活性的影响,果胶酶活性是试验指标。(单指标试验,多指标试验)
77. 试验因素:凡对试验指标可能产生影响的原因或要素。 如:酱油质量受原料、曲种、发酵时间等的影响,这些都是影响酱油质量的因素。
78. 因素水平:试验因素所处的某种特定状态或数量等级。 如:比较3个大豆品种蛋白质含量高低,这3个品种就是大豆品种这个试验因素的三个水平
79. 试验处理:事先设计好的实施在实验单位上的一种具体措施或项目。 如:单因素试验中,试验因素的一个水平就是一个处理 多因素:水平组合
80.
平方和与自由度分解:设一个试验共有k个处理n个重复,则该试验资料共有nk个观测值,其数据分组如下:
81. F值:两个方差之比。 F=
82. F自由度:两个。df1= dft=k-1 df2= dfe=k(n-1)
83. F检验:用F值出现概率的大小推断两个方差是否相等的方法。
84. 方差分析表:
变异来源
平方和(SS)
自由度(df)
均分(MS)
F值
处理间
SSt
dft=k-1
MSt=SSt/dft
SSt/SSe
处理内
SSe=SST-SSt
dfe=dfT-dft
MSe=SSe/dfe
总变异
SST
dfT=nk-1
85. 线性模型:被分析的变量总体中每一个变数可以按其变异的原因分解成若干个线性组成部分。
86. 单因素线性模型的数学模型可归纳为:1.效应的可加性 2.分布的正态性 3.方差的同质性
87. 多重比较:统计学中把多个平均数两两间的比较。(F值显著或极显著否定了无效假设H0,表明试验的总变异主要来源于处理间的变异。)(常用的有最小显著差数法(LSD法)和最小显著极差法(LSR法)。)
88.
最小显著差数法(LSD法)的检验程序:在处理间的F检验显著的前提下,计算出显著水平为a的最小显著差数LSDa;任何两个处理平均数间的差数
,若其绝对值≥LSDa,则为在
水平上差异显著;反之,则为在
水平上差异不显著。这种方法又称为保护性最小显著差数法。LSD法实质上是t检验。
89. 最小显著极差法(LSR法)特点:把相互比较的两平均数的差数看成是平均数的极差,根据极差范围捏所包含的处理数K(称为秩次距)的不同而采用不同的检验尺度,以克服LSD法的不足。
90. 最小显著极差法: q检验和新复极差法。
91. q检验法:检验统计量为q值。 q=R/
92. 新复极差法(邓肯氏法,SSR):
93. 各处理重复数相等的方差分析:
94. 两向分组资料的方差分析
1.
两向分组单独观测值试验资料的方差分析
95. 简单效应:在某因素同一水平上,另一因素不同水平对试验指标的影响。
96. 主效应:由于因素水平的改变而引起的平均数的改变量。
97. 互作效应:在多因素试验中,一个因素的作用要受到另一个因素的影响,表现为某一因素在另一因素的不同水平上所产生的效应不同。
2. 两因素等重复试验:
98. 两向分组有重复资料方差分析时数据总变异原因可以分解为:A因素,B因素,A*B和误差

99. 方差分析的基本假定:1.效应的可加性 2.分布的正态性 3.方差的同质性
100. 参数统计:限定分布的估计或检验。
101. 非参数统计:对总体分布的具体形式不必作任何限制性假定和不以总体参数具体数值估计或检验为目的的推断统计。
102. 非参数统计检验:非参数统计主要用于对某种判断或假设进行检验。
103. x2检验
104. 适应性检验:判断实际观察次数属性分配是否依循已知属性分配理论或学说的一种假设检验方法。
105. 独立性检验:用x2检验来探求两因子间是否彼此独立还是关联的检验。
106. 相关系数的回归系数的符号:无法判断
107. 线性回归分析中的假设检验:检验变量x和y是否有线性相关关系。
第八章
108. 试验指标:根据研究目的而选定的用来衡量或考核试验效果的质量特性。(如:考察加热对果 胶酶活性的影响,果胶酶活性是试验指标)
109. 试验因素:凡对试验指标可能产生影响的原因或要素。(如:酱油质量受原料、曲种、发酵时 间等的影响,这些都是影响酱油质量的因素。)
110. 因素水平:试验因素所处的某种特定状态或数量等级。(如:比较3个大豆品种蛋白质含量高 低,这3个品种就是大豆品种这个试验因素的三个水平)
111. 试验处理:事先设计好的实施在实验单位上的一种具体措施或项目。(如:单因素试验中, 试验因素的一个水平就是一个处理)
112. 试验单位:在试验中能接受不同实验处理的独立的试验载体。
113. 重复:在一个试验中,将一个处理实施在两个或两个以上的试验单位上。
114. 处理:是指事先设计好的实施在试验单位上的一种具体措施。
115. 全面试验:试验中,对所选取的试验因素的所有水平组合全部给予实施的试验。
116. 部分实施(部分试验):从全部试验处理中选取部分有代表性的处理进行试验。
117. 试验设计的三原则:重复,随机化,局部控制
第十一章
118. 正交设计:利用正交表来安排与分析多因素试验的一种设计方法。
119. 正交设计的基本特点:用部分试验来代替全面试验,通过对部分试验结果的分析,了解全面试验的情况。
120.
正交表
: L表示正交表,n表示试验点数,即正交表行数,t表示因素的水平数,q为最多能安排的因素数,即正交表列数。
121. 正交表的性质: 1.任何一列中各水平都出现,且出现次数相等。
2.任意两列间各种不同水平的所有可能组合都出现,且出现次数相等。
122. 正交设计的基本步骤:
1) 明确实验目的,确定实验目标
2) 挑因素,选水平 (水平2~4个,不超过6个)
3) 选择合适的正交表 (在能够安排下试验因素和交互作用的前提下,因素的个数不大于正交表记号中括号内的指数,
要考虑的因素及交互作用的自由度总和小于所选正交表的总自由度)
4) 进行表头的设计 1.只考察主效应,不考虑互作效应的表头设计。
2.只考虑互作效应的表头设计。
5) 确定试验方案,实施试验
6) 试验结果分析
123. 表头设计:将试验因素安排到所选正交表的各列中去的过程。
124. 交互作用:指因素间的联合搭配而产生的对试验指标的影响作用。
125. 相关系数:是表示两个变量间线性相关的程度和性质的统计量。
限时特惠:本站每日持续更新5-20节内部创业项目课程,一年会员
只需199元,全站资源免费下载点击查看详情
站长微信:
jjs406





