线性代数是数学的一个分支,它的研究对象是向量,向量空间(或称线性空间),线性变换和有限维的线性方程组。线性代数在物理学、密码学、人工智能、虚拟现实中具有广泛的应用,它的计算方法在计算数学中占据了重要的地位。目前,它已经应用于自然科学和社会科学的各个学科当中。
一、n阶行列式的定义
全排列:把n个不同的元素排成一列。n个不同元素的全排列个数为:
自然排列:n个元素由小到大排列的序列,称为标准次序。
逆序:如果一个排列
中出现
,则称他们组成一个逆序。寻找逆序的方法是统计当前元素的前面比自己大的元素的个数。
逆序数:排列中所有元素的逆序数之和。计算方法为:从左往右依次计算每个元素的逆序数,然后求和得到排列的逆序数。
奇排列和偶排列:排列的逆序数为奇数,就是奇排列;否则,就是偶排列。
定理1:对于n个元素的排列,奇排列和偶排列各占一半,个数为
定理2:如果排列中两个元素发生一次互换,那么排列的奇偶性就会变化。
n阶行列式:n阶行列式(Determinant)是把nxn个元素(数字或表达式等)排成n行n列,如下图所示。
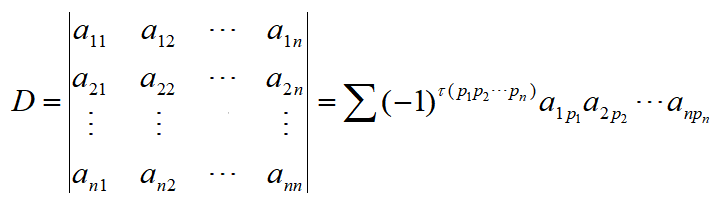
它的值所有取自不同行不同列的n个元素的乘积的代数和。公式的记忆方法:行标是自然排列,列标是1-n的全排列,符号根据列标全排列的奇偶性来确定。同理,由于排列的对换原理,可以得到行列式的另外两个定义:
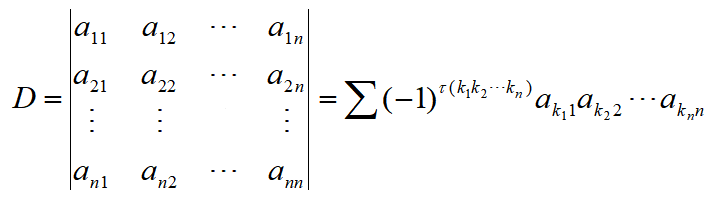
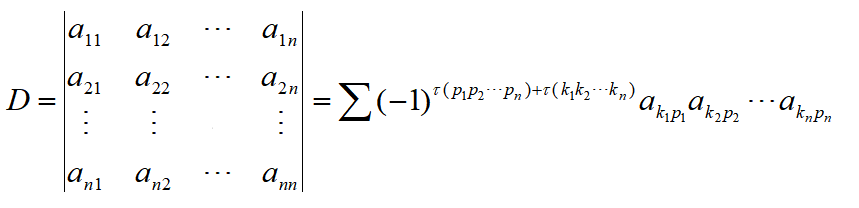
其中,第三种是n阶行列式的一般定义。计算中,通常采用第一种或第二种,多数教材采用的是第一种定义。
二、n阶行列式的性质
性质1:行列式和它的转置行列式相等
性质2:行列式某行(或某列)元素有公因子,可以提到行列式符号的外面
性质3:行列式某行(或某列)如果是两数之和,可以按此行将行列式拆成两个行列式之和,其他行保持不变
性质4:互换行列式的两行(或两列),行列式变号
性质5:行列式中有两行(或两列)对应元素都相等,则行列式为0
性质6:行列式中的两行(或两列)对应元素成比例,则行列式为0
性质7:把行列式中的某一行(或列)各个元素乘以同一个数(非0)加到另一行(或列)对应的元素上,行列式的值不变。
性质8:如果行列式某行(或某列)元素全部都是0,则行列式为0
三、行列式按行(列)展开
余子式:在n阶行列式中划去元素
所在的行和列的所有元素,剩余元素按原来顺序排列组成一个(n-1)阶的行列式,这个行列式就是
的余子式,记为
。
代数余子式:在余子式前冠以符号
,则称之为代数余子式,记为
。因此,可以得到下面的关系:
引理:如果n阶行列式D的第i行只有元素
不为0,那么行列式的值等于:
定理1:n阶行列式D等于它任意一行各元素与其对应代数余子式的乘积之和。
同理,可以得到行列式的按列展开形式:
定理2:n阶行列式D的某一行(列)的元素与另一行(列)对应元素的代数余子式的和等于0。(原理是另一行元素被本行元素取代了,新行列式中两行相等了)
综合展开定理1和定理2,可以得到两个重要结论:
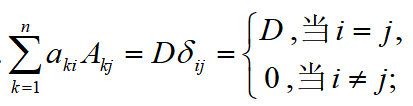
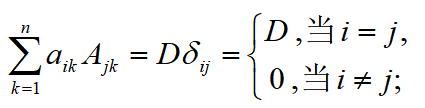
拉普拉斯定理:在n阶行列式中任选r行,然后从这r行中任选r列,构成一个r阶子式,根据组合原理,这样的r阶子式共有
个,分别记为M1,M2……,其代数余子式记作A1,A2……,那么
四、行列式的计算方法
方法1:二、三阶行列式可以使用对角线法则
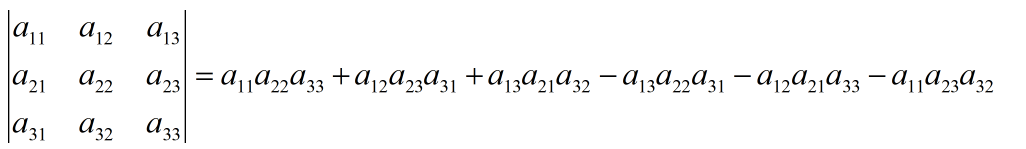
例1:计算二阶行列式
例2:计算三阶行列式
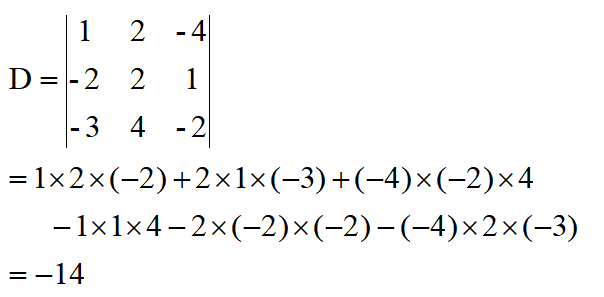
方法2:0非常多的行列式可以考虑使用定义
使用方法:从0最多的行(或列)开始确定元素,选择非0元素。
例3:
由于选择第一行的0对于计算没有任何意义,因此可以确定第一行必选1(a14位置),选中后将此元素对应的行和列划去。再从第二行选择,选择非0元素2(a23位置),划去第2行和第3列;以此类推,根据定义:
例4:
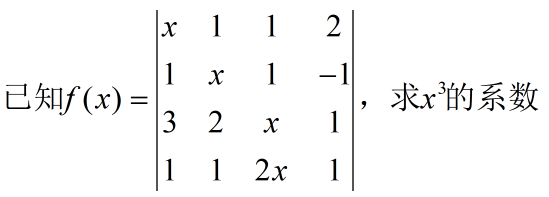
解:求三次方项的系数,那么第一二行的两个x是必须选中的,否则无法得到3次方项。第三行和第4行都有一个x,那么选择方法有两种:
因此,两项合并之后,三次方项的次数为-1。
方法3:特殊行列式
特殊行列式包括:上三角行列式、下三角行列式、对角行列式
上三角行列式:主对角线元素的乘积
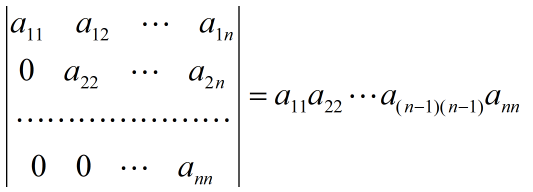
下三角行列式:主对角线元素的乘积
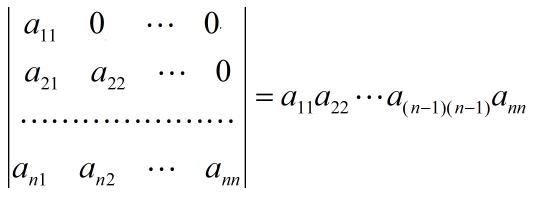
副对角线上的三角矩阵:副对角线元素的乘积,符号与阶数相关。
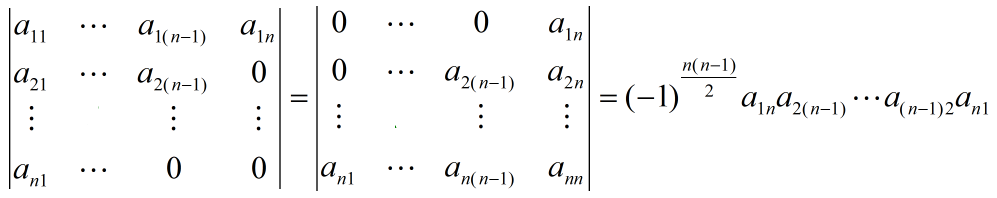
对角行列式是上面4种特殊行列式的特例,因此计算方法完全一致。
例5:计算行列式
解:左边行列式=1 x 2 x 3 x 4 = 24
右边行列式= -1x 2 x (-3) =6
例6:计算行列式
解:过程如下
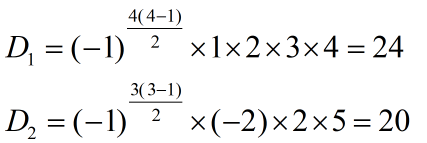
例7:计算行列式
解:答案和例6一致。
例8:计算行列式
解:计算如下:
方法4:使用性质计算行列式
(1)利用性质7
技巧:将行列式化为上三角行列式或者下三角行列式
例9:计算行列式
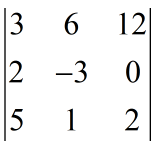
解:计算过程如下
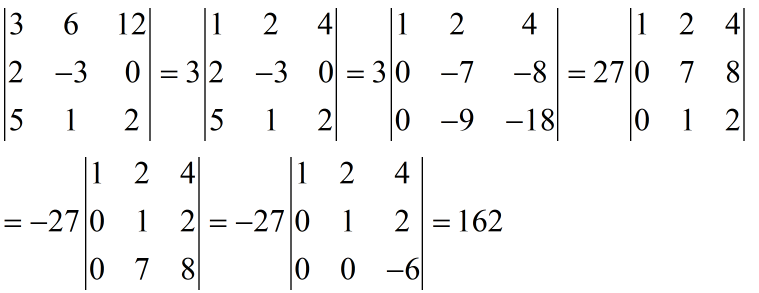
(2)“行(列)和相等”的行列式
技巧:先把所有的行(列)都往第一行(列)上加,然后提取公因子
例10:计算行列式
解:计算过程如下:
同理,可以将其他行加到第一行,然后提取公因子。
(3)

型行列式
技巧:使用对角元素消去第一行或第一列(依次将各列【行】的某个倍数加到第一列【行】)
例11:计算行列式
解:依次将各列的-1倍加到第一列:
方法5:降阶法
技巧:用0比较多的行进行展开
(1)普通降阶计算
例12:计算行列式
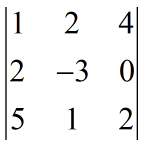
解:直接按照第3列展开:
(2)
型行列式(两线一点)
技巧:按照有点的那一行(列)展开
例13:计算行列式
解:按照第一例展开:
方法6:递推法
(1)

型行列式(双线+一横或一竖)
技巧:和”两线一点“类型的行列式一样,从只有两个元素的列(行)展开,然后可以找规律递推。
例14:计算行列式
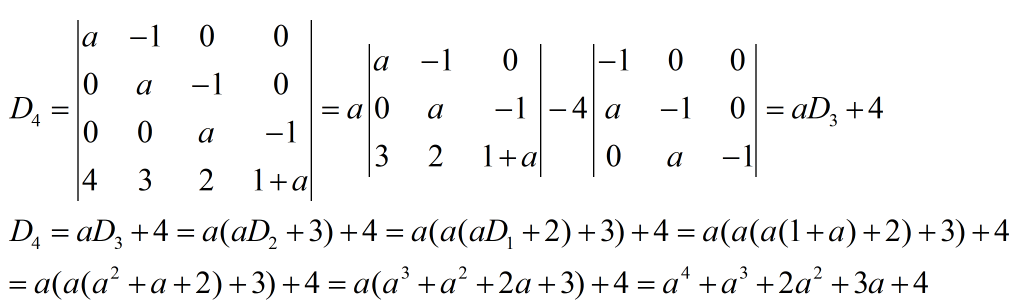
(2)
型不等式(三线型)
技巧:递推法,然后使用特征根法(递推法)求解。
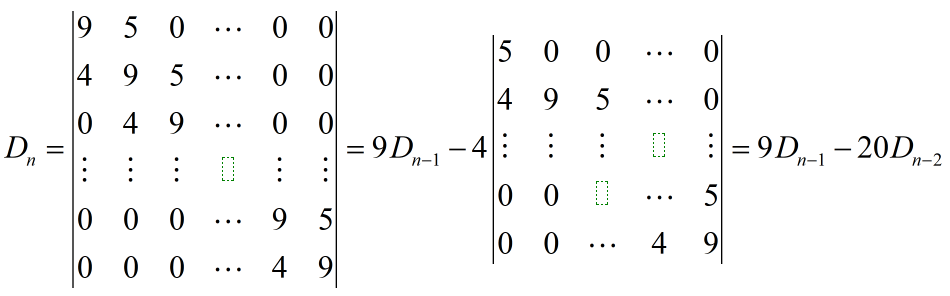
此递推式可以使用递推法或者特征根法,特征解得如下:
因此,可以得到通项公式:

方法7:升阶法
技巧:如果行列式中相同得元素很多而且有显著得规律,通过升阶法,通常会将行列式变成

型行列式
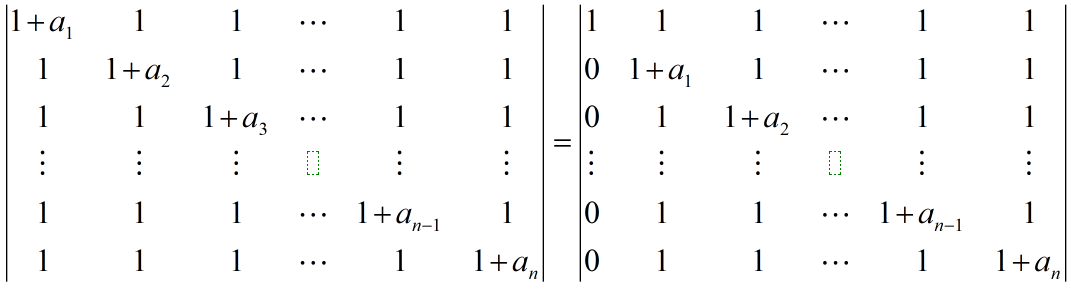

方法8:数学归纳法
技巧:先计算1阶和2阶行列式,然后假设k阶成立,证明(k+1)阶成立。这类行列式有明显的递推规律。
(1)范德蒙德行列式
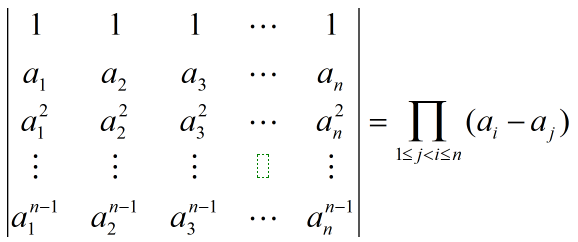
证明:数学归纳法

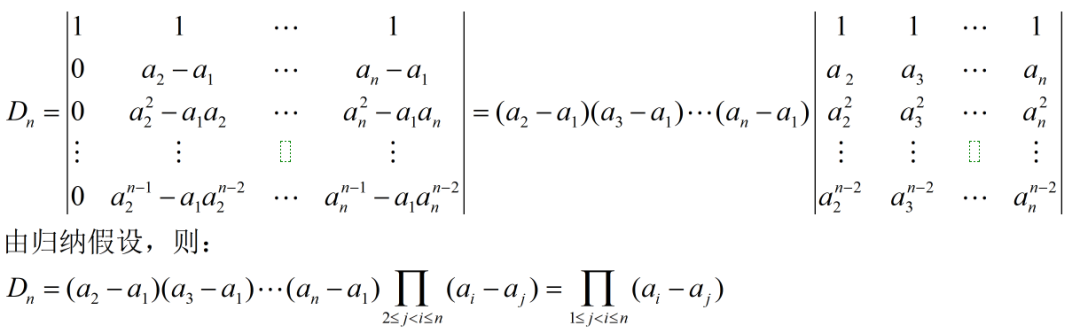
记忆方法:将第二行元素依次排列,使用后面的元素减去第一个位置的元素,然后将删除这个元素,重复上述操作,直到只剩下2个元素为止。因此,总共有n(n-1)/2项。
范德蒙德行列式的应用:
(1)计算行列式
解:第二行元素分别时2、3、4、5,那么按照依次相减的策略,得到:
五、克拉默(克莱姆)法则
定理(Cramer法则):如果线性方程组
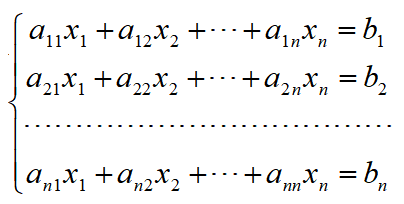
的系数行列式
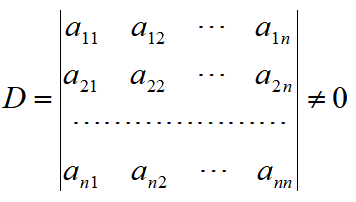
那么,这个方程组有唯一解:
其中,分子
就是用常数项将系数行列式的第j列替换掉得到的新行列式。
值得注意的是:
1、如果系数行列式为0,不能使用克拉默法则
2、如果方程个数和未知数个数不相等,不能使用克拉默法则
例题:使用克拉默法则解方程组
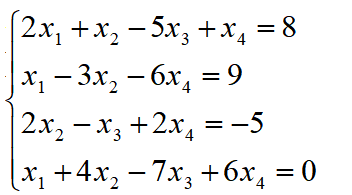
解:首先计算系数行列式
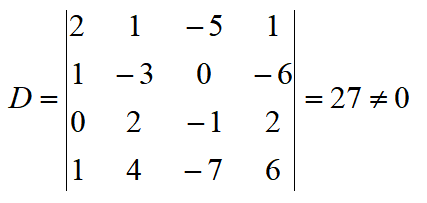
因此,该方程组可以使用克拉默法则进行计算。下面使用常数项替换系数行列式的第一列:
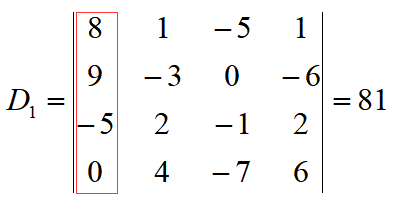
于是可以得到x1的值:
同理,替换系数行列式的第2列,可以得到:

计算得到x2的值:
同理,可以计算出所有的未知数的解:
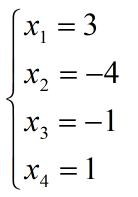
限时特惠:本站每日持续更新5-20节内部创业项目课程,一年会员
只需199元,全站资源免费下载点击查看详情
站长微信:
jjs406





