学习那些事
反三角函数是一种基本初等函数
它是反正弦arcsin x,反余弦arccos x,反正切arctan x,反余切arccot x,反正割arcsec x,反余割arccsc x这些函数的统称,表示角
三角函数的反函数是个多值函数,其图像与其原函数关于函数 y=x 对称。
函数可分为单值函数和多值函数
单值函数:对定义域内每个自变量x,其对应的函数值f(x)是唯一的,如y=x。
多值函数:多值函数是函数的扩充,一个自变量对应多个因变量,如|y|=x。
反三角函数广泛应用于工程,导航,物理和几何
本文将介绍
反正弦函数
反正弦函数
记作y=arcsinx或siny=x(x∈[-1,1])
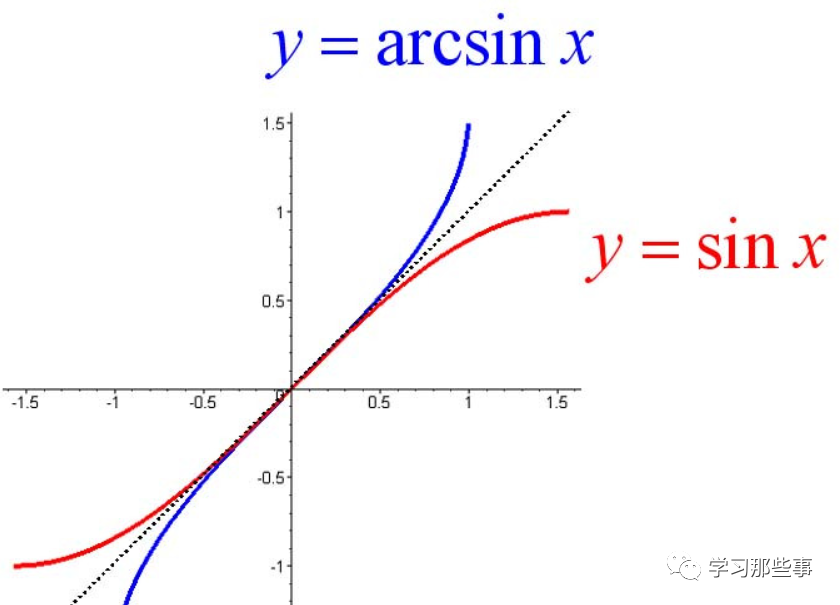
图像特点:关于一三象限角平分线对称
由图得该函数单调递增
应用:当三角形边的长度已知时,尝试确定直角三角形的剩余两个角度时
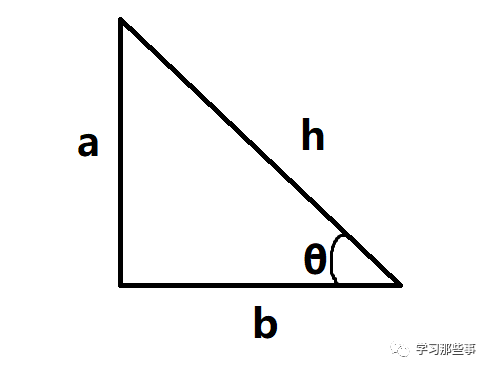
有:θ=arcsin(a/h)
反余弦函数
反余弦函数
记作y=arccosx或cosy=x(x∈[-1,1])
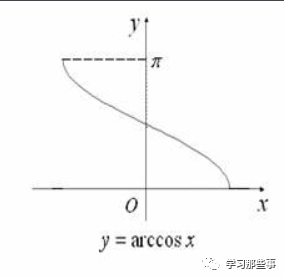
由图得该函数单调递减
反正切函数
反正切函数
记作y=arctanx 或 y=tan-1x
是正切函数y=tanx在开区间(x∈(-π/2,π/2))的反函数,表示在定义域上正切值等于 x 的那个唯一确定的角
由于正切函数y=tanx在定义域R上不具有一一对应的关系,所以不存在反函数。
这里选取是正切函数的一个单调区间。反正切函数是存在且唯一确定的。
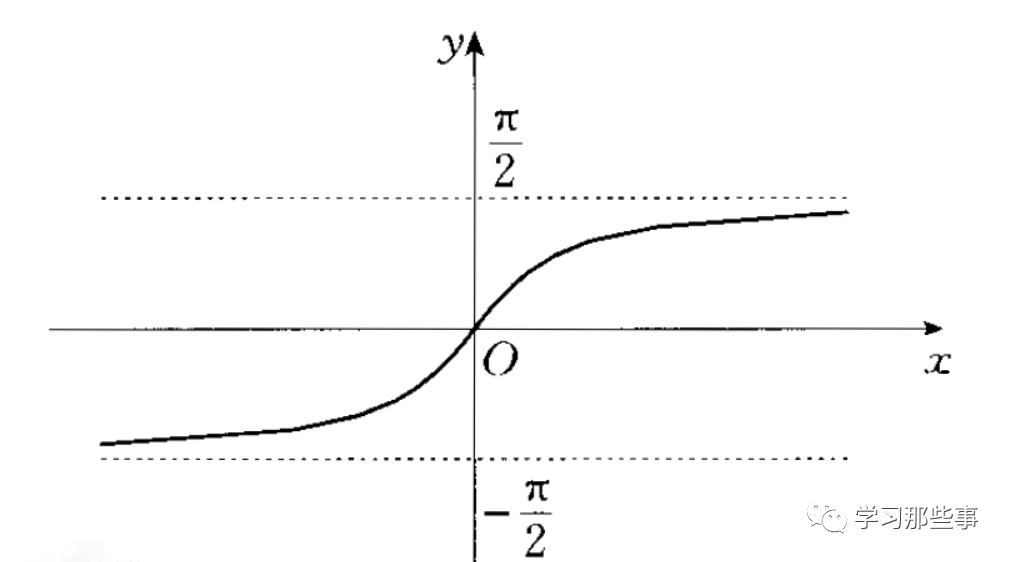
大致图像如上图
由图得该函数单调递减
应用:通常,斜边是未知的,需要使用毕达哥拉斯定理(勾股定理)在使用反正弦或反曲线之前进行计算:a2+b2=h2,其中h是斜边的长度。
在这种情况下,反正切是有用的,因为斜边的长度是不需要的
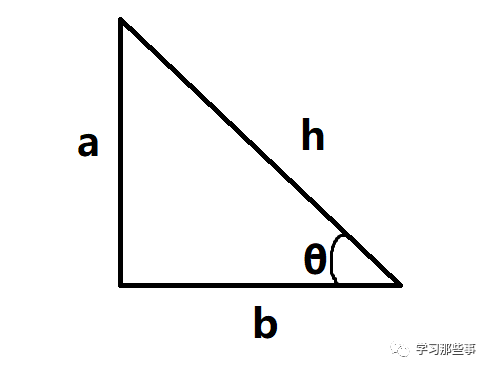
θ=arcsin(a/b),省略了计算h的步骤
好了分享就到这里,请关注我们!以后会持续分享一些与学习有关的文章。想要看什么可以后台留言
(不限学科)
学习那些事
限时特惠:本站每日持续更新5-20节内部创业项目课程,一年会员
只需199元,全站资源免费下载点击查看详情
站长微信:
jjs406





