正态性和方差齐性是经典统计模型应用的两个前提条件,所谓正态性,严格来说是残差要符合正态性分布,不过实际中大部分情况下是对因变量进行正态性检验。而方差齐性就是要求方差相等,意思是对于每一个x取值,因变量的方差基本相等,本节内容先阐述正态性。
用统计检验方法判断正态性
目前大部分统计学软件的正态性检验方法有如下4种:Shapiro-Wilk(SW)检验、Kolmogorov-Smirnov(KS)检验、Cramer-von Mises(CVM)检验和Anderson-Darling(AD)检验。根据其思想大致可分为以下两类:
1.基于峰度和偏度的SW检验
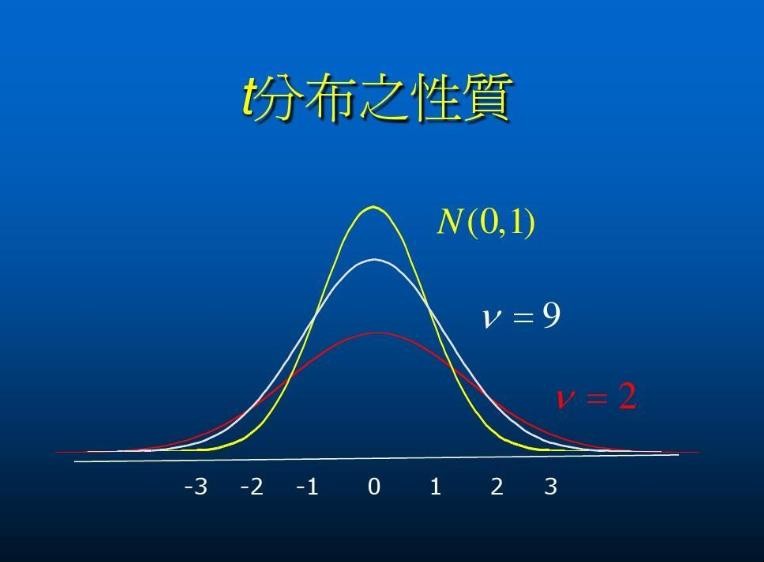
SW检验的思想是基于偏离峰度或和偏度,峰度通俗来讲就是分布形状是平坦还是尖峰,偏度则反映了分布形状是否对称,也就是说峰度和偏度分别从上下和左右两个维度来说明分布是否符合正态分布。
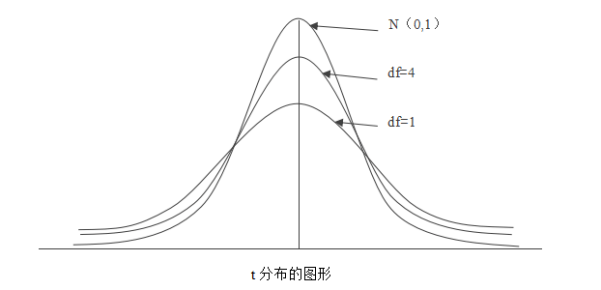
正态分布的峰度和偏度均为0,如果峰度大于0则提示为尖峰,如果峰度小于0则提示为平坦峰,如果偏度大于0则提示为右偏态(正偏态),如果偏度小于0则提示为左偏态(负偏态)。
SW检验反映了基于峰度和偏度对正态分布的偏离程度,该值介于0到1之间,越接近1,说明越符合正态分布,越接近0,说明越符合偏态分布。
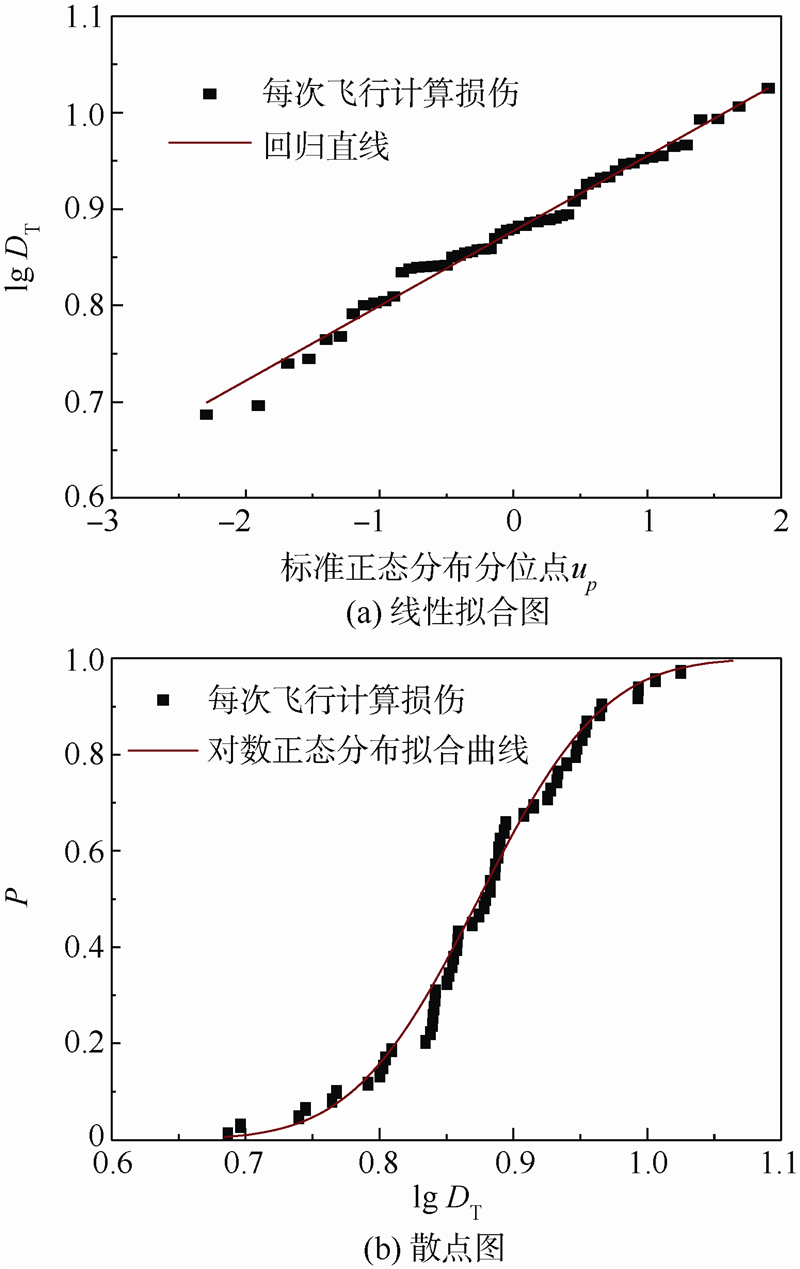
2.基于拟合优度的KS、CVM和AD检验
上述三种检验都是基于拟合优度的思想,计算理论分布与基于数据得到的分布之间的差异,给予这种思想,它们的主要区别在于对差别的定义,如KS法定义理论分布与实际数据分布的差别是绝对值形式,而CVM法是平方的形式,AD法则是对CVM法进一步做出了改进。
当以上四种方法的结果不一致时,需要考虑如下:如果例数在2000以内,则SW检验的效率最高,一般建议作为首选方法,而在基于拟合优度的方法中,AD法效率最高,KS法效率最低。
Ref: 《白话统计》冯国双著
限时特惠:本站每日持续更新5-20节内部创业项目课程,一年会员
只需199元,全站资源免费下载点击查看详情
站长微信:
jjs406





