初中数学|因式分解常用七大解题方法,分类讲解+例题解析,收藏
多项式的因式分解是代数式恒等变形的基本形式之一,这是初中基础代数学习的主要方法,是我们解决许多数学问题的有力工具.因式分解的方法灵活多变,技巧性极强,学习和掌握这些方法与技巧,不仅是掌握因式分解内容所必需的,而且对于培养同学们的解题技能,提升同学们的思维能力,都有着比较重要的作用。

初中数学中主要学习了提取公式法、运用公式法、分组分解法和十字相乘法,唐老师将在中学数学课本的基础上,对因式分解的方法、技巧和应用作进一步的深度学习与讲解,帮助大家掌握因式分解的技巧。
一、提公因式法.:ma+mb+mc=m(a+b+c)
二、运用公式法.
在整式的乘、除中,我们学过若干个乘法公式,现将其反向使用,即为因式分解中常用的公式,例如:
(1)(a+b)(a-b) = a2-b2 ———a2-b2=(a+b)(a-b);
(2) (a±b)2 = a2±2ab+b2 ——— a2±2ab+b2=(a±b)2;
(3) (a+b)(a2-ab+b2) =a3+b3—— a3+b3=(a+b)(a2-ab+b2);
(4) (a-b)(a2+ab+b2) = a3-b3 ——a3-b3=(a-b)(a2+ab+b2).
下面再补充两个常用的公式:
(5)a2+b2+c2+2ab+2bc+2ca=(a+b+c)2;
(6)a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca);

三、分组分解法
(一)分组后能直接提公因式
比如,从“整体”看,这个多项式的各项既没有公式可提,也不能运用公式分解,但从“局部”看,这个多项式前两项都含有a,后两项都含有b,因此可以考虑将前两项分为一组,后两项分为一组先分解,然后再考虑两组之间的联系。

(二)分组后能直接运用公式
分组后能直接运用公式,主要是通过对题目当中各因式的观察,进行分组后,能够进行公因式分解,直到分解的最后能够变成几个多项式或单项式与多项式的乘积为止。


综合练习:
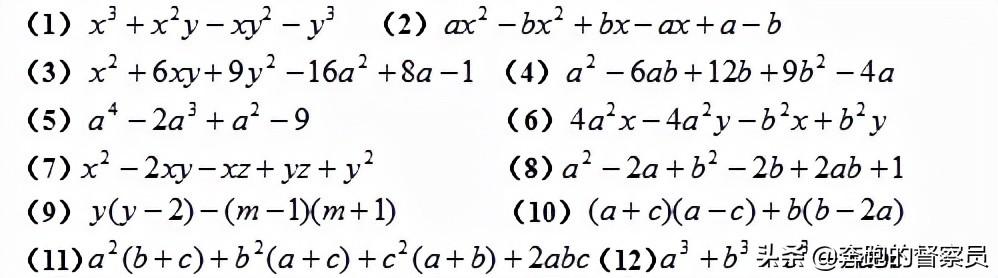
四、十字相乘法.
十字相乘法是因式分解当中比较难的一种分解方式。在运用过程当中,对同学们的思维提出了更高的要求,等大家都熟练了这种方法以后,其实对于因式分解是非常简单的,而且比较方便。

对于十字相乘法,我们分为四种类型。给大家做详细的讲解。针对每一种方法都有经典的例题解析,通过例题解析的方式让大家明白因式分解时该如何操作,遵循怎样的分解步骤,才能比较顺利的解决和掌握十字相乘法。
(一)二次项系数为1的二次三项式
直接利用公式——进行分解。
特点:(1)二次项系数是1;
(2)常数项是两个数的乘积;
(3)一次项系数是常数项的两因数的和。

(二)二次项系数不为1的二次三项式
(三)二次项系数为1的齐次多项式

(四)二次项系数不为1的齐次多项式

五、换元法。

换元法在因式分解当中,其难度较大,主要是根据因式分解的要求,对于公因式当中出现了比较大的数字或多项式时,同学们很难在短时间内看到十字相乘法的简单形式,所以通过换元的方式,把相同的多项式或数字用简单的字母来代替,这样对于用十字相乘法时更加的明显,也比较简单,最后再将换元的形式补充回来,就可以得到最后因式分解的形式,这种方法在解题时能极大的提高同学们的解题效率,而且从形式上会使原来的式子变得更加的简单。

六、添项、拆项、配方法。
天象拆项配方法是在以上几种方法进行因式分解未果的情况下才考虑的因式分解的另一种形式。这种分配的方式其难度以及要求的思维能力比起前面的几种方式都比较高。学习这几种方法,一定在平时就要加强训练,把这种方法灵活运用能力提高到新的高度,否则当真正遇到这类题型时,很难快速的得到解决的方案,以至于降低了学习效率。
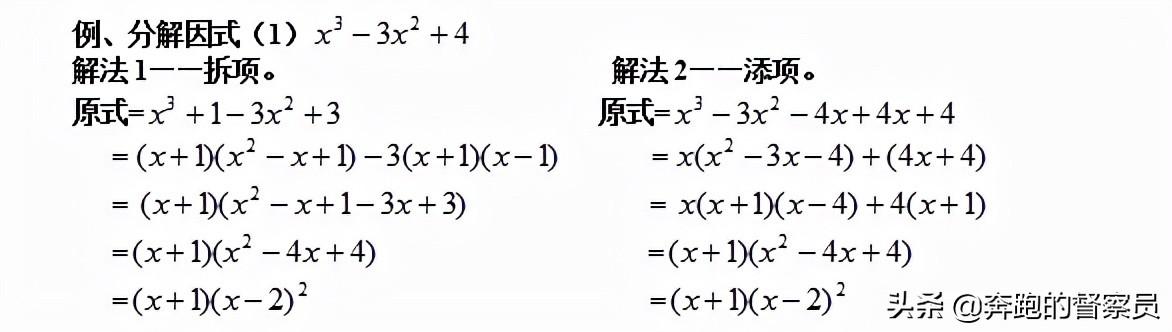
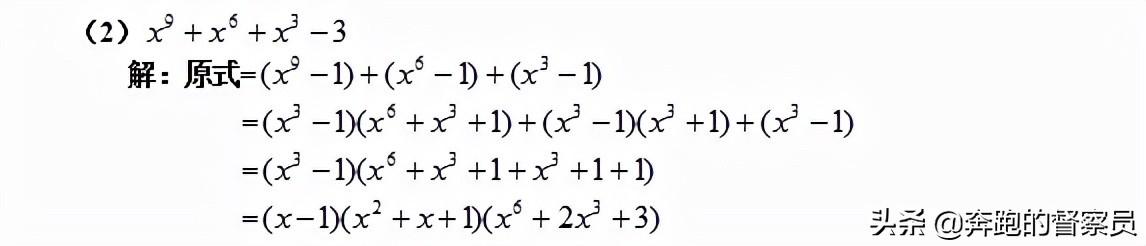
七、待定系数法。
待定系数法在因式分解的方法当中算是独一份。主要是采用逆向思维的方法,从猜想到的结论当中进行。解方程的形式来得到因式分解的结果,这种方法对于提升同学们的数学思维有比较好的促进作用,建议想要提升数学思维的同学,进行加强练习。

在一般的分解因式当中,这种方法能用到的频率并不高,但是对于有关因式分解中求参数的知识运用比较广泛,具体的方法,我们通过经典的例题解析来给大家一一呈现。
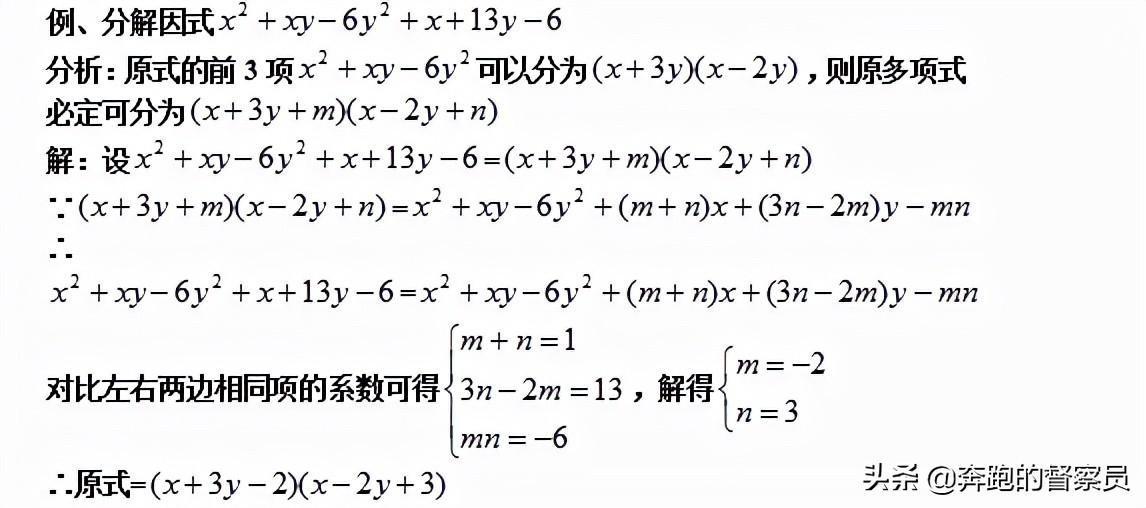
请输入描述


写在最后:通过以上唐老师给大家讲解的有关初中数学因式分解的七种方法,这七种方法当中,各种方法都有自己的优势。在遇到题目时,需要进行因式分解,我们可以根据题目的特点,选用自己熟悉的方法进行解题即可,各种方法都有自己的优势,想要拓展思维提升,知识运用能力的同学,一定要一一进行学习,掌握其中解题的技巧,这对于拓展思维提升数学思维能力,能起到非常好的作用。
限时特惠:本站每日持续更新5-20节内部创业项目课程,一年会员
只需199元,全站资源免费下载点击查看详情
站长微信:
jjs406





